题目内容
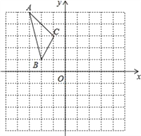
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
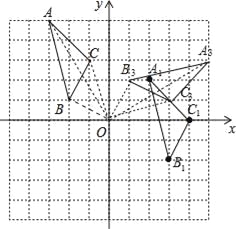
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
【答案】(1)点A1的坐标为(2,2),B1点的坐标为(3,﹣2);(2)A2(3,﹣5),B2(2,﹣1),C2(1,﹣3);(3)△A2B3C3为所作,A3(5,3),B3(1,2),C3(3,1);
【解析】试题分析:(1)利用点C和点C1的坐标变化得到平移的方向与距离,然后利用此平移规律写出顶点A1,B1的坐标;
(2)根据关于原点对称的点的坐标特征求解;
(3)利用网格和旋转的性质画出△A2B3C3,然后写出△A2B3C3的各顶点的坐标.
试题解析:(1)如图,△A1B1C1为所作,
因为点C(﹣1,3)平移后的对应点C1的坐标为(4,0),
所以△ABC先向右平移5个单位,再向下平移3个单位得到△A1B1C1,
所以点A1的坐标为(2,2),B1点的坐标为(3,﹣2);
(2)因为△ABC和△A1B2C2关于原点O成中心对称图形,
所以A2(3,﹣5),B2(2,﹣1),C2(1,﹣3);
(3)如图,△A2B3C3为所作,A3(5,3),B3(1,2),C3(3,1);

练习册系列答案
相关题目