题目内容
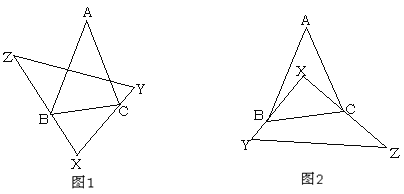
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB交CB的延长线于点G.

(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据已知条件证明BE=DF,BE∥DF,从而得出四边形DFBE是平行四边形,即可证明DE∥BF,
(2)先证明DE=BE,再根据邻边相等的平行四边形是菱形,从而得出结论.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵点E、F分别是AB、CD的中点,
∴BE=![]() AB,DF=
AB,DF=![]() CD.
CD.
∴BE=DF,BE∥DF,
∴四边形DFBE是平行四边形,
∴DE∥BF;
(2)∵∠G=90°,AG∥BD,AD∥BG,
∴四边形AGBD是矩形,
∴∠ADB=90°,
在Rt△ADB中
∵E为AB的中点,
∴AE=BE=DE,
∵四边形DFBE是平行四边形,
∴四边形DEBF是菱形.

练习册系列答案
相关题目
【题目】下表是全国7个城市2017年3月份某日空气质量指数(AQI)的统计结果:
城市 | 北京 | 成都 | 深圳 | 长沙 | 上海 | 武汉 | 广州 |
AQI指数 | 25 | 72 | 49 | 241 | 62 | 185 | 49 |
该日空气质量指数的中位数是( )
A. 49 B. 62 C. 241 D. 97