题目内容
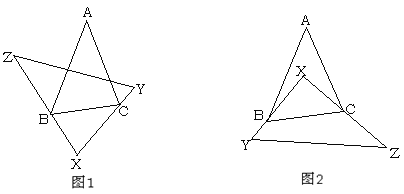
【题目】已知:在△ABC和△XYZ中,∠A=40°,∠Y+∠Z=95°,将△XYZ如图摆放,使得∠X的两条边分别经过点B和点C.
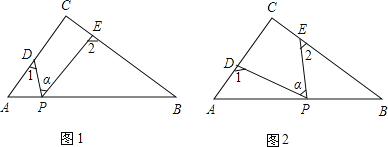
(1)当将△XYZ如图1摆放时,则∠ABX+∠ACX=_____________度;
(2)当将△XYZ如图2摆放时,请求出∠ABX+∠ACX的度数,并说明理由;
(3)能否将△XYZ摆放到某个位置时,使得BX、CX同时平分∠ABC和∠ACB?请直接写出你的结论:___________
【答案】(1)235°;
(2)∠ABX+∠ACX=45°.理由见解析;
(3)不能
【解析】试题分析:(1)要求∠ABX+∠ACX的度数,只要求出∠ABC+∠CBX+∠ACB+∠BCX,利用三角形内角和定理得出∠ABC+∠ACB=180°-∠A=180°-40°=140°;根据三角形内角和定理,∠CBX+∠BCX=∠Y+∠Z=95°,∴∠ABX+∠ACX=∠ABC+∠CBX+∠ACB+∠BCX=140°+95°=235°;(2)要求∠ABX+∠ACX的度数,只要求出∠ABC+∠ACB-(∠BCX+∠CBX)的度数.根据三角形内角和定理,∠CBX+∠BCX=∠Y+∠Z=95°;根据三角形内角和定理得,∠ABC+∠ACB=180°-∠A=140°,∴∠ABX+∠ACX=∠ABC+∠ACB-(∠BCX+∠CBX)=140°-95°=45°;(3)不能.假设能将△XYZ摆放到某个位置时,使得BX、CX同时平分∠ABC和∠ACB.则∠CBX+∠BCX=∠ABX+∠ACX=95°,那么∠ABC+∠ACB=190°,与三角形内角和定理矛盾,所以不能.
试题解析:(1)在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=40°
∴∠ABC+∠ACB=180°40°=140°
在△BCX中,∠X+∠BCX+∠CBX=180°
∴∠BCX+∠CBX=180°∠X
在△XYZ中,∠X+∠Y+∠Z=180°
∴∠Y+∠Z=180°∠X
∴∠CBX+∠BCX=∠Y+∠Z=95°
∴∠ABX+∠ACX=∠ABC+∠CBX+∠ACB+∠BCX=140°+95°=235°;
(2)∠ABX+∠ACX=45度。理由如下:
∵∠Y+∠Z=95°
∴∠X=180°(∠Y+∠Z)=85°
∴∠ABX+∠ACX=180°∠A∠XBC∠XCB=180°40°(180°85°)=45°;
(3)不能。假设能将△XYZ摆放到某个位置时,使得BX、CX同时平分∠ABC和∠ACB.则∠CBX+∠BCX=∠ABX+∠ACX=95°那么∠ABC+∠ACB=190°,与三角形内角和定理矛盾,所以不能。