题目内容
【题目】阅读下列两则材料,回答问题:
材料一:平面直角坐标系中,对点A(x1,y1),B(x2,y2)定义一种新的运算:AB=x1x2+y1y2,例如:若A(1,2),B(3,4),则AB=1×3+2×4=11
材料二:平面直角坐标系中,过横坐标不同的两点A(x1,y1),B(x2,y2)的直线的斜率为kAB=![]() ,由此可以发现:若kAB=
,由此可以发现:若kAB=![]() =1,则有y1﹣y2=x1﹣x2,即x1﹣y1=x2﹣y2,反之,若x1,x2,y1,y2,满足关系式x1﹣y1=x2﹣y2,则有y1﹣y2=x1﹣x2,那么kAB=
=1,则有y1﹣y2=x1﹣x2,即x1﹣y1=x2﹣y2,反之,若x1,x2,y1,y2,满足关系式x1﹣y1=x2﹣y2,则有y1﹣y2=x1﹣x2,那么kAB=![]() =1.
=1.
(1)已知点M(﹣2,﹣6),N(3,﹣2),则MN= ,若点A,B的坐标分别为(x1,y1),(x2,y2)(x1≠x2),且满足关系式2x1+y1=2x2+y2,那么kAB= ;
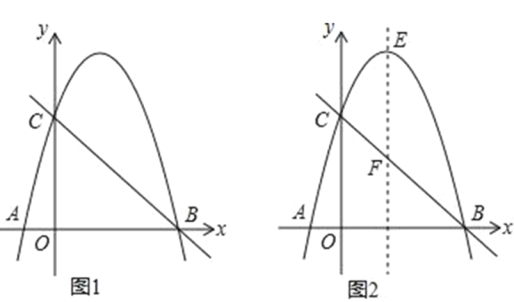
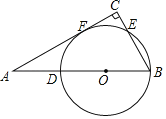
(2)如图,横坐标互不相同的三个点C,D,E满足CD=DE,且D点是直线y=x上第一象限内的点,点D到原点的距离为2![]() .过点D作DF∥y轴,交直线CE于点F,若DF=6,请结合图象,求直线CE、直线DF与两坐标轴围成的四边形面积.
.过点D作DF∥y轴,交直线CE于点F,若DF=6,请结合图象,求直线CE、直线DF与两坐标轴围成的四边形面积.
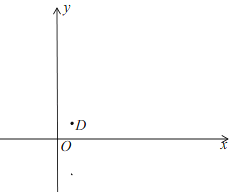
【答案】(1)6,﹣2;(2)四边形OMFH的面积为6或8.
【解析】
(1)根据材料一和材料二计算即可;
(2)由CD=DE,且D点的坐标为(2,2),得出x1+y1=x2+y2,即可得出直线CE的斜率为kCE=﹣1,分两种情形分别求出直角梯形的面积即可解决问题.
解:(1)根据新的运算,MN=﹣2×3+(﹣6)×(﹣2)=6;
∵点A,B的坐标分别为(x1,y1),(x2,y2)(x1≠x2),且满足关系式2x1+y1=2x2+y2
∴y1﹣y2=﹣2(x1﹣x2),
∴kAB=![]() ;
;
故答案为6,﹣2.
(2)设点C,E的坐标分别为(x1,y1),(x2,y2)(x1≠x2),
∵点D在直线y=x上,OD=2![]() ,
,
∴D(2,2),
∵CD=DE,D点的坐标为(2,2),
∴2x1+2y1=2x2+2y2,即x1+y1=x2+y2,
由(1)可知:直线CE的斜率为kCE=﹣1,
∵DF=6,
∴DH=2,HF=4,OM=2,
∴直线CE、直线DF与两坐标轴围成的四边形OMFH的面积=![]() (2+4)×2=6
(2+4)×2=6
或直线CE、直线DF与两坐标轴围成的四边形OM′F′H的面积=![]() (10+8)×2=18,
(10+8)×2=18,
综上所述,直线CE、直线DF与两坐标轴围成的四边形OMFH的面积为6或8.