题目内容
【题目】如图所示,在Rt△ABC中,∠C=90°,BC=6,AC=8, P是斜边AB上一动点,PD⊥AC于点D,PE⊥BC于点E,则DE的长不可能是( )
A.4B.5C.6D.7
【答案】A
【解析】
连接CP,根据矩形的性质可知:DE=CP,当DE最小时,则CP最小,根据垂线段最短可知当CP⊥AB时,则CP最小,再根据三角形的面积为定值即可求出CP的长,从而求出DE的最小值,再进行判断即可.
∵Rt△ABC中,∠C=90°,AC=8,BC=6,
∴AB=10,
连接CP,
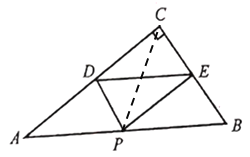
∵PD⊥AC于点D,PE⊥CB于点E,
∴四边形DPEC是矩形,
∴DE=CP,
当CP最小时,则DE最小,根据垂线段最短可知当CP⊥AB时,则CP最小,
∴![]() ,
,
在四个选项中,只有选项A的值小于4.8,因此,选项A符合题意,
故选:A.

练习册系列答案
相关题目
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象上部分点的横坐标x与纵坐标y的对应值如下表所示:
x | … | -1 | 0 | 2 | 4 | … |
y | … | -5 | 1 | 1 | m | … |
求:(1)这个二次函数的解析式;
(2)这个二次函数图象的顶点坐标及上表中m的值.