题目内容
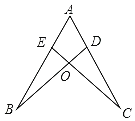
【题目】如图,E是平行四边形ABCD的边AD上的一动点(点E不与A、D重合),连结CE并延长交BA的延长线于点F。
(1) △CDE与△FAE是否总相似?为什么?
(2)当E点为AD的中点时,求证:CE=EF;
(3)当E点移至使EC⊥BC时,设AB=4cm,EF=6cm,∠D=60°时,求CB的长。(结果不取近似值)

【答案】(1)相似;(2)证明△CDE≌△FAE;(3)2+2![]()
【解析】
⑴根据两个角相等求证三角形相似;
⑵当E点为AD的中点时,DE=AE,再根据全等三角形的性质求证.
⑶根据相似三角形的性质得出△DEC∽△FBC,再根据直角三角形的勾股定理比例得出CE,DE的值,同理根据△DEC∽△FBC得出![]() =
=![]() ,代入求值即可.
,代入求值即可.
⑴总是相似,∵CD∥AB,∴∠D=∠EAF,∵∠DEC=∠AEF,∴△DEC∽△AEF.
⑵当E点为AD的中点时,DE=AE,∴△DEC≌△AEF,∴CE=EF.
⑶设CE为x,DE为y,当E点移至使EC⊥BC时,∠BCF=∠AEF=90°,∵∠D=60°,∴∠B=60°,∵∠DEC=∠BCF=∠AEF=90°,∴△CDE∽△CBF,∵EF=6,AB=CD=4,∠DEC=90°,根据直角三角形的勾股定理得![]() =
=![]() ,
,![]() =
=![]() ,则 DE=2,CE=2
,则 DE=2,CE=2![]() ,又∵∠BCF=∠CED,∠CDE=∠B,∴△DEC∽△FBC,则
,又∵∠BCF=∠CED,∠CDE=∠B,∴△DEC∽△FBC,则![]() =
=![]() ,∴CB=2+2
,∴CB=2+2![]() .
.

练习册系列答案
相关题目