题目内容
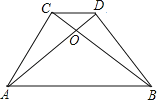
【题目】如图,边长为4的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上.动点D在线段BC上移动(不与B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE.
(1)当CD=1时,求点E的坐标;
(2)如果设CD=t,梯形COEB的面积为S,那么是否存在S的最大值?若存在,请求出这个最大值及此时t的值;若不存在,请说明理由.

【答案】(1)(4,![]() );(2)S=
);(2)S=![]() +2t+8,当t=2时有最大值10.
+2t+8,当t=2时有最大值10.
【解析】
根据相似三角形判定定理得两个直角三角形相似,再根据性质定理解出E点坐标;结合梯形面积的计算公式得到函数再求最值.
因为DE⊥OD,所以∠ODB=90![]() , ∠ODC+∠BDE=90
, ∠ODC+∠BDE=90![]() ,在三角形OCD中,∠ODC+∠COD=90
,在三角形OCD中,∠ODC+∠COD=90![]() ,所以∠BDE=∠COD,同理得∠CDO=∠BED,由相似三角形判定定理得△OCD
,所以∠BDE=∠COD,同理得∠CDO=∠BED,由相似三角形判定定理得△OCD![]() △DBE,
△DBE,![]() ,BE=
,BE=![]() ,AE=4-
,AE=4-![]() , E的坐标为(4,
, E的坐标为(4,![]() );设CD=t,DB=4-t,由
);设CD=t,DB=4-t,由![]() 得BE=t-
得BE=t-![]() , 则梯形COEB的面积为S=
, 则梯形COEB的面积为S=![]() +2t+8=
+2t+8=![]() ,当t=2时有最大值10.
,当t=2时有最大值10.

练习册系列答案
相关题目
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?