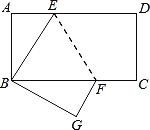
题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,边长为
,边长为![]() 的正方形的一个顶点
的正方形的一个顶点![]() 在边
在边![]() 上,与
上,与![]() 另两边分
另两边分

别交于点![]() 、
、![]() ,
,![]() ,将正方形平移,使点
,将正方形平移,使点![]() 保持在
保持在![]() 上(
上(![]() 不与
不与![]() 重合),设
重合),设![]() ,正方形与
,正方形与![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
![]() 求
求![]() 与
与![]() 的函数关系式并写出自变量
的函数关系式并写出自变量![]() 的取值范围;
的取值范围;
![]() 为何值时
为何值时![]() 的值最大?
的值最大?
![]() 在哪个范围取值时
在哪个范围取值时![]() 的值随
的值随![]() 的增大而减小?
的增大而减小?
【答案】(1)![]() ,自变量
,自变量![]() 的取值范围是
的取值范围是![]() ;(2)当
;(2)当![]() 时,
时,![]() 有最大值;(3)当
有最大值;(3)当![]() 时,
时,![]() 随
随![]() 的增大而减小.
的增大而减小.
【解析】
(1)当点![]() 保持在
保持在![]() 上时,正方形与
上时,正方形与![]() 重叠部分为直角梯形
重叠部分为直角梯形![]() ,根据直角梯形的面积公式,只需用含
,根据直角梯形的面积公式,只需用含![]() 的代数式分别表示出上底
的代数式分别表示出上底![]() 、下底
、下底![]() 及高
及高![]() 的长度即可.由
的长度即可.由![]() 为等腰直角三角形,可得高
为等腰直角三角形,可得高![]() ,则
,则![]() ,下底
,下底![]() ,进而得到
,进而得到![]() ,再根据等腰三角形及平行线的性质可证
,再根据等腰三角形及平行线的性质可证![]() ,得出上底
,得出上底![]() ,根据点
,根据点![]() 保持在
保持在![]() 上,且
上,且![]() 不与
不与![]() 重合,可知
重合,可知![]() ,从而求出自变量
,从而求出自变量![]() 的取值范围;
的取值范围;
(2)由(1)知,![]() 是
是![]() 的二次函数,根据二次函数的性质,可知当
的二次函数,根据二次函数的性质,可知当![]() 时,
时,![]() 的值最大;
的值最大;
(3)根据二次函数的增减性,当![]() 时,在对称轴
时,在对称轴![]() 的右侧,
的右侧,![]() 的值随
的值随![]() 的增大而减小.
的增大而减小.
解:![]() ∵
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵点![]() 保持在
保持在![]() 上,且
上,且![]() 不与
不与![]() 重合,
重合,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
故![]() ,自变量
,自变量![]() 的取值范围是
的取值范围是![]() ;
;
![]() ∵
∵![]() ,
,
∴当![]() 时,
时,![]() 有最大值;
有最大值;
![]() ∵
∵![]() ,
,![]() ,
,![]() ,
,
∴当![]() 时,
时,![]() 随
随![]() 的增大而减小.
的增大而减小.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?