Question

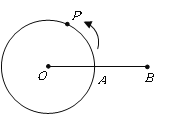
【题目】如图，是半径为的上的定点，动点从出发，以的速度沿圆周逆时针运动，当点回到地立即停止运动．

（1）如果，求点运动的时间；

（2）如果点是延长线上的一点，，那么当点运动的时间为时，判断直线与的位置关系，并说明理由．

Answer 1

【答案】（1）或（2）直线与相切，理由见解析

【解析】

（1）当∠POA=90°时，点P运动的路程为⊙O周长的或，所以分两种情况进行分析；
（2）直线BP与⊙O的位置关系是相切，根据已知可证得OP⊥BP，即直线BP与⊙O相切．

解：（1）当∠POA=90°时，根据弧长公式可知点P运动的路程为⊙O周长的或，设点P运动的时间为ts；
当点P运动的路程为⊙O周长的时，2πt=2π12，
解得t=3；
当点P运动的路程为⊙O周长的时，2πt=2π12，
解得t=9；
∴当∠POA=90°时，点P运动的时间为3s或9s．
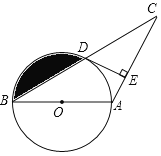
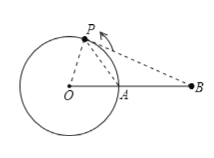
（2）如图，当点P运动的时间为2s时，直线BP与⊙O相切
理由如下：
当点P运动的时间为2s时，点P运动的路程为4πcm，
连接OP，PA；
∵半径AO=12cm，
∴⊙O的周长为24πcm，
∴的长为⊙O周长的，
∴∠POA=60°；
∵OP=OA，
∴△OAP是等边三角形，
∴OP=OA=AP，∠OAP=60°；
∵AB=OA，
∴AP=AB，
∵∠OAP=∠APB+∠B，
∴∠APB=∠B=30°，
∴∠OPB=∠OPA+∠APB=90°，
∴OP⊥BP，
∴直线BP与⊙O相切．