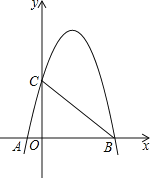题目内容
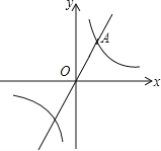
【题目】 如图,已知正比例函数y=kx与反比例函数y=![]() 的图象在第一象限交于点A(2,4).
的图象在第一象限交于点A(2,4).
(1)求正比例函数与反比例函数的解析式.
(2)平移直线OA,平移后的直线与x轴交于点B,与反比例函数的图象交于第一象限的点C(4,n).
①求直线BC的解析式;
②线段BC的长是______.
【答案】(1)正比例函数的解析式为y=2x,反比例函数的解析式为y=![]() ;(2)①y=2x-6;②
;(2)①y=2x-6;②![]() .
.
【解析】
(1)将点A的坐标分别代入y=kx与y=![]() ,即可得出正比例函数与反比例函数的解析式;
,即可得出正比例函数与反比例函数的解析式;
(2)①利用已知的反比例函数的解析式,可得出n的值;设平移后的一次函数解析式,代入点C的坐标,即可得出直线BC的解析式;
②先求出点B的坐标,再利用两点间的距离公式,即可得出线段BC的长.
解:(1)∵正比例函数y=kx与反比例函数y=![]() 的图象在第一象限交于点A(2,4),
的图象在第一象限交于点A(2,4),
∴4=2k,4=![]() ,
,
解得:k=2,m=8,
∴正比例函数的解析式为y=2x,反比例函数的解析式为y=![]() ;
;
(2)①∵点C(4,n)在反比例函数y=![]() 的图象上,
的图象上,
∴n=![]() =2,
=2,
即点C的坐标为(4,2).
∵AO∥BC,
∴可设直线BC的解析式为y=2x+b,
又点C(4,2)在直线BC上,
∴2=2×4+b,
解得b=-6,
即直线BC的解析式为y=2x-6;
②∵直线BC与x轴交于点B,
∴当y=0时,0=2x-6,
解得x=3,
∴点B的坐标为(3,0),
∵C(4,2),
∴BC=![]() =
=![]() .
.
故答案为![]() .
.

练习册系列答案
相关题目