题目内容
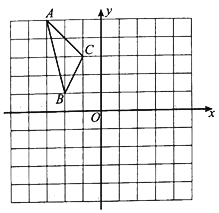
【题目】如图,在平面直角坐标系中,A(6,0),B(6,3),画出△ABO的所有以原点O为位似中心的△CDO,且△CDO与△ABO的相似比为1:3,并写出C、D的坐标.
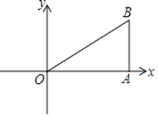
【答案】△CDO见详解;点C坐标为(2,0),点D坐标为(2,1)或C(-2,0),D(-2,-1).
【解析】
利用位似比分别得出符合题意的两种图形即可,利用相似三角形的性质求解可得C与D的坐标.
解;如图所示:两种情况,
∵A(6,0),B(6,3),
∴OA=6,AB=3,
∵△CDO与△ABO的相似比为1:3,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
解得:OC=2,CD=1,
∴C(2,0),D(2,1);
同理知C′(-2,0),D′(-2,-1).
综上,点C坐标为(2,0),点D坐标为(2,1)或C(-2,0),D(-2,-1).
故答案为:△CDO见详解;点C坐标为(2,0),点D坐标为(2,1)或C(-2,0),D(-2,-1).

练习册系列答案
相关题目