��Ŀ����
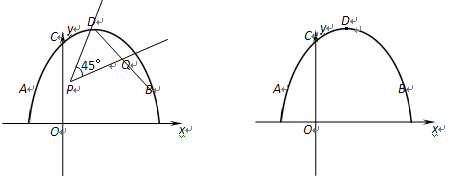
��ͼ��������![]() �Ķ���ΪD����x�ύ�ڵ�A��B����y�ύ�ڵ�C����OB = 2OC= 3��
�Ķ���ΪD����x�ύ�ڵ�A��B����y�ύ�ڵ�C����OB = 2OC= 3��
��1����a��b��ֵ��
��2����45��ǵĶ���P���߶�OB�ϻ���(�����B�غ�)���ýǵ�һ�߹���D����һ����BD���ڵ�Q����P��x��0����y2=![]() DQ�������y2����x�ĺ�����ϵʽ��
DQ�������y2����x�ĺ�����ϵʽ��
��3����ͬһƽ��ֱ������ϵ�У�����ֱ��x = m��x = m+![]() �ֱ���������y1���ڵ�E��G����y2�ĺ���ͼ���ڵ�F��H���ʵ�E��F��H��GΧ���ı��ε�����ܷ�Ϊ
�ֱ���������y1���ڵ�E��G����y2�ĺ���ͼ���ڵ�F��H���ʵ�E��F��H��GΧ���ı��ε�����ܷ�Ϊ![]() �����ܣ����m��ֵ�������ܣ���˵�����ɣ�
�����ܣ����m��ֵ�������ܣ���˵�����ɣ�
��������ͨ��B(3��0)��C(0��![]() )���㣬��������ߵĽ���ʽ��
)���㣬��������ߵĽ���ʽ��
��2����DN��AB����y1���AB=4��DN=BN=2��DB=2![]() ���ɸ��ݹ��ɶ�����jPD2-(1-x)2=4������Ϊ��MPQ�� ��MBP������kPD2=DQ´DB=
���ɸ��ݹ��ɶ�����jPD2-(1-x)2=4������Ϊ��MPQ�� ��MBP������kPD2=DQ´DB=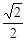 y2´2
y2´2![]() ����j��k��y2��x�ĺ�����ϵʽ
����j��k��y2��x�ĺ�����ϵʽ
��3������E��F��H��GΧ���ı��ε������Ϊ![]() ��ͨ��y1���E��G��F��H�����꣬���EF��GH�ij��ȣ�
��ͨ��y1���E��G��F��H�����꣬���EF��GH�ij��ȣ�
ͨ���ı���EFHG��������m��ֵ
��1������֪��OB=2OC=3
�ɵã�������y1=ax2-2ax+b����B(3��0)��C(0��![]() )���㣬
)���㣬
��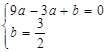 ����
����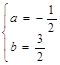
�������ߵĽ���ʽΪy1= -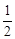 x2+x+
x2+x+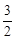 �� ---------4��
�� ---------4��
��2����DN��AB������ΪN��������ͼ1��
��y1= -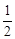 x2+x+
x2+x+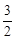 ��D(1��2)�� N(1��0)��A(-1��0)��B(3��0)��
��D(1��2)�� N(1��0)��A(-1��0)��B(3��0)��
��AB=4��DN=BN=2��DB=2![]() ��
��
ÐDBN=45�㣮���ݹ��ɶ�����BD 2-BN 2=PD 2-PN 2��
��(2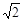 )2-22=PD2-(1-x)2-----j
)2-22=PD2-(1-x)2-----j
��ÐMPQ=45��=ÐMBP��
���MPQ �� ��MBP����PD2=DQ´DB=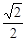 y2´2
y2´2![]() ------k��
------k��
��j��k��y2=![]() x2-x+
x2-x+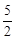 ����0��x��3��
����0��x��3��
��y2��x�ĺ�����ϵʽΪy2=![]() x2-x+
x2-x+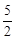 =
=![]()
![]() (0��x��3)��--------4��
(0��x��3)��--------4��
���Ա���ȡֵ��Χûд�����۷֣�
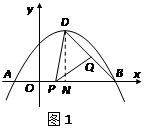

��3������E��F��H��GΧ���ı��ε������Ϊ![]() ����ͼ2��
����ͼ2��
�ߵ�E��G��������y1= -![]() x2+x+
x2+x+![]() =
=![]() �ֱ���ֱ��x=m��x= m+
�ֱ���ֱ��x=m��x= m+![]() �Ľ���
�Ľ���
���E��G����Ϊ E(m��![]() )��G(m+
)��G(m+![]() ��
��![]() )��
)��
ͬ������F��H���� ΪF(m��![]() )��H(m+
)��H(m+![]() ��
��![]() )��
)��
��EF=![]() -��
-��![]() ��=
��=![]()
GH=![]() )-��
)-��![]() ��=
��=![]() ��
��
���ı���EFHG��ƽ���ı��λ����Σ�
��S=![]() ��
��![]() +
+![]() �ݡ�
�ݡ�![]() =
=![]()
�����![]()
���m=![]() ��
��![]() ������0��x��3�ڣ�
������0��x��3�ڣ�
���ԣ���m=![]() ��
��![]() ʱ��E��F��H��GΧ���ı��ε����Ϊ
ʱ��E��F��H��GΧ���ı��ε����Ϊ![]() . --------4��
. --------4��

 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
�����ܿ����ϵ�д� �㣮
�㣮 21����ͼ�������ߵĶ���ΪA��1��-4�����ҹ���B��3��0����
21����ͼ�������ߵĶ���ΪA��1��-4�����ҹ���B��3��0���� ��2013•���ϣ���ͼ�������ߵĶ���ΪP��-2��2������y�ύ�ڵ�A��0��3������ƽ�Ƹ�������ʹ�䶥��P��ֱ���ƶ�����P�䣨2��-2������A�Ķ�Ӧ��ΪA�䣬����������PA��ɨ����������Ӱ���֣������Ϊ
��2013•���ϣ���ͼ�������ߵĶ���ΪP��-2��2������y�ύ�ڵ�A��0��3������ƽ�Ƹ�������ʹ�䶥��P��ֱ���ƶ�����P�䣨2��-2������A�Ķ�Ӧ��ΪA�䣬����������PA��ɨ����������Ӱ���֣������Ϊ ��2013•��üɽ�ж�ģ����֪����ͼ�������ߵĶ���ΪC��1��-2����ֱ��y=kx+m�������߽���A��B���㣬����OA=3��B����y���ϣ���PΪ�߶�AB�ϵ�һ�����㣨��P���A��B���غϣ�������P�Ҵ�ֱ��x���ֱ�������������߽��ڵ�E��
��2013•��üɽ�ж�ģ����֪����ͼ�������ߵĶ���ΪC��1��-2����ֱ��y=kx+m�������߽���A��B���㣬����OA=3��B����y���ϣ���PΪ�߶�AB�ϵ�һ�����㣨��P���A��B���غϣ�������P�Ҵ�ֱ��x���ֱ�������������߽��ڵ�E��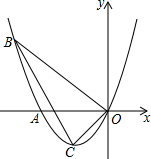 ��2013•������˹����ͼ�������ߵĶ���ΪC��-1��-1�����Ҿ�����A����B������ԭ��O����B�ĺ�����Ϊ-3��
��2013•������˹����ͼ�������ߵĶ���ΪC��-1��-1�����Ҿ�����A����B������ԭ��O����B�ĺ�����Ϊ-3��