题目内容
 (2013•河南)如图,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,-2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为
(2013•河南)如图,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,-2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为12
12
.分析:根据平移的性质得出四边形APP′A′是平行四边形,进而得出AD,PP′的长,求出面积即可.
解答: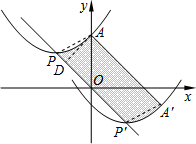 解:连接AP,A′P′,过点A作AD⊥PP′于点D,
解:连接AP,A′P′,过点A作AD⊥PP′于点D,
由题意可得出:AP∥A′P′,AP=A′P′,
∴四边形APP′A′是平行四边形,
∵抛物线的顶点为P(-2,2),与y轴交于点A(0,3),平移该抛物线使其顶点P沿直线移动到点P′(2,-2),
∴PO=
=2
,∠AOP=45°,
∴△ADO是等腰直角三角形,
∴PP′=2
×2=4
,
∴AD=DO=
×3=
,
∴抛物线上PA段扫过的区域(阴影部分)的面积为:4
×
=12.
故答案为:12.
 解:连接AP,A′P′,过点A作AD⊥PP′于点D,
解:连接AP,A′P′,过点A作AD⊥PP′于点D,由题意可得出:AP∥A′P′,AP=A′P′,
∴四边形APP′A′是平行四边形,
∵抛物线的顶点为P(-2,2),与y轴交于点A(0,3),平移该抛物线使其顶点P沿直线移动到点P′(2,-2),
∴PO=
| 22+22 |
| 2 |
∴△ADO是等腰直角三角形,
∴PP′=2
| 2 |
| 2 |
∴AD=DO=
| ||
| 2 |
3
| ||
| 2 |
∴抛物线上PA段扫过的区域(阴影部分)的面积为:4
| 2 |
3
| ||
| 2 |
故答案为:12.
点评:此题主要考查了二次函数图象与几何变换以及平行四边形面积求法和勾股定理等知识,根据已知得出AD,PP′是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
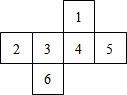 (2013•河南)如图是正方体的一种展开图,其每个面上都标有一个数字,那么在原正方体中,与数字“2”相对的面上的数字是( )
(2013•河南)如图是正方体的一种展开图,其每个面上都标有一个数字,那么在原正方体中,与数字“2”相对的面上的数字是( )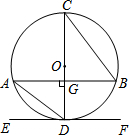 (2013•河南)如图,CD是⊙O的直径,弦AB⊥CD于点G,直线EF与⊙O相切于点D,则下列结论中不一定正确的是( )
(2013•河南)如图,CD是⊙O的直径,弦AB⊥CD于点G,直线EF与⊙O相切于点D,则下列结论中不一定正确的是( )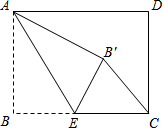 (2013•河南)如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为
(2013•河南)如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为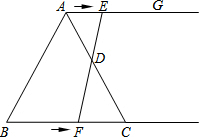 (2013•河南)如图,在等边三角形ABC中,BC=6cm.射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(2013•河南)如图,在等边三角形ABC中,BC=6cm.射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).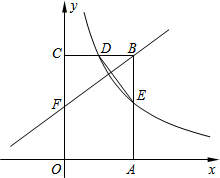 (2013•河南)如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3).双曲线y=
(2013•河南)如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3).双曲线y=