题目内容
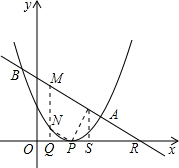
如图,抛物线的顶点为P(1,0),一条直线与抛物线相交于A(2,1),B(-| 1 | 2 |
 点.
点.(1)求抛物线和直线AB的解析式;
(2)若M为线段AB上的动点,过M作MN∥y轴,交抛物线于点N,连接NP、AP,试探究四边形MNPA能否为梯形?若能,求出此点M的坐标;若不能,请说明理由.
分析:(1)可先根据P点的坐标,用顶点式二次函数通式设出抛物线的解析式,然后将A点的坐标代入抛物线中,即可求出二次函数的解析式,进而可求得B点的坐标.然后根据A、B两点的坐标求出直线AB的解析式.
(2)可假设存在这样的点M,若四边形MNPA为梯形,那么只有一种可能即NP∥MA,可通过构建相似三角形来求出N点的坐标.由于N点在抛物线上,因此可根据抛物线的解析式设出N点的坐标,假设直线AB与x轴的交点为R(R的坐标可通过直线AB的解析式求得),过A作AS⊥x轴于S,可通过证三角形NPQ和ARS相似来得出关于NQ,AS,QP,SR的比例关系式,据此可求出N点的横坐标,然后将N点的横坐标代入直线AB的解析式中即可求出M的坐标.
(2)可假设存在这样的点M,若四边形MNPA为梯形,那么只有一种可能即NP∥MA,可通过构建相似三角形来求出N点的坐标.由于N点在抛物线上,因此可根据抛物线的解析式设出N点的坐标,假设直线AB与x轴的交点为R(R的坐标可通过直线AB的解析式求得),过A作AS⊥x轴于S,可通过证三角形NPQ和ARS相似来得出关于NQ,AS,QP,SR的比例关系式,据此可求出N点的横坐标,然后将N点的横坐标代入直线AB的解析式中即可求出M的坐标.
解答:解:(1)由题意,可设抛物线的解析式为y=a(x-1)2.
∴a(2-1)2=1,
∴a=1
∴抛物线的解析式为y=x2-2x+1.(1分)
当x=-
时,m=(-
)2-2×(-
)+1=
,
设直线AB的解析式为y=kx+b
∴
,
解得
.
∴直线AB的解析式为y=-
x+2.
(2)假设符合条件的点M存在.
由题意可知,MN不平行于AP,
∴梯形的两底只能是NP、MA.
设AB与x轴相交于点R,MN的延长线与x轴相交于点Q,作AS⊥x轴于点S,
 由y=-
由y=-
x+2知点R的坐标为(4,0).
∵NP∥MA
∴∠NPQ=∠ARS,
∵∠NQP=∠ASR=90°
∴Rt△NPQ∽Rt△ARS
∴
=
设N点的坐标为(x,x2-2x+1),
则有
=
,
解得x=
,x=1(舍去).
当x=
时,y=-
×
+2=
.
∴符合条件的点M存在,其坐标为(
,
).
∴a(2-1)2=1,
∴a=1
∴抛物线的解析式为y=x2-2x+1.(1分)
当x=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
设直线AB的解析式为y=kx+b
∴
|
解得
|
∴直线AB的解析式为y=-
| 1 |
| 2 |
(2)假设符合条件的点M存在.
由题意可知,MN不平行于AP,
∴梯形的两底只能是NP、MA.
设AB与x轴相交于点R,MN的延长线与x轴相交于点Q,作AS⊥x轴于点S,
 由y=-
由y=-| 1 |
| 2 |
∵NP∥MA
∴∠NPQ=∠ARS,
∵∠NQP=∠ASR=90°
∴Rt△NPQ∽Rt△ARS
∴
| NQ |
| AS |
| QP |
| SR |
设N点的坐标为(x,x2-2x+1),
则有
| x2-2x+1 |
| 1 |
| 1-x |
| 2 |
解得x=
| 1 |
| 2 |
当x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 4 |
∴符合条件的点M存在,其坐标为(
| 1 |
| 2 |
| 7 |
| 4 |
点评:本题考查了一次函数和二次函数解析式的确定、相似三角形的判定和性质、梯形的判定和性质等知识点.
主要考查学生数形结合的数学思想方法.
主要考查学生数形结合的数学思想方法.

练习册系列答案
相关题目
 21、如图,抛物线的顶点为A(1,-4),且过点B(3,0).
21、如图,抛物线的顶点为A(1,-4),且过点B(3,0). (2013•河南)如图,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,-2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为
(2013•河南)如图,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,-2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为 (2013•峨眉山市二模)已知,如图,抛物线的顶点为C(1,-2),直线y=kx+m与抛物线交于A、B两点,其中OA=3,B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.
(2013•峨眉山市二模)已知,如图,抛物线的顶点为C(1,-2),直线y=kx+m与抛物线交于A、B两点,其中OA=3,B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.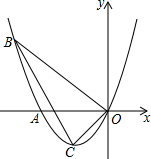 (2013•鄂尔多斯)如图,抛物线的顶点为C(-1,-1),且经过点A、点B和坐标原点O,点B的横坐标为-3.
(2013•鄂尔多斯)如图,抛物线的顶点为C(-1,-1),且经过点A、点B和坐标原点O,点B的横坐标为-3.