题目内容
【题目】如图,AB∥CD∥EF,CD交AF于G,
(1)如图1,若CF平分∠AFE,∠A=70°,求∠C;
(2)如图2,请写出∠A,∠C和∠AFC的数量关系并说明理由.
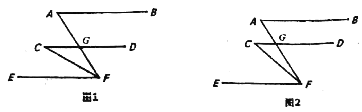
【答案】(1)∠C=35°;(2)∠A=∠C+∠AFC. 理由见解析.
【解析】
(1)由平行线的性质可求出∠AFE=70°,由角平分线的定义可求∠CFE=35°,然后再根据平行线的性质即可求出求∠C;
(1)由AB∥CD,可得∠DGF=∠A,由三角形外角的性质可得∠DGF=∠C+∠AFC,进而可求出∠A,∠C和∠AFC的数量关系.
(1)∵AB∥EF, ∠A=70°,
∴∠AFE=∠A=70°,
∵CF平分∠AFE,
∴∠CFE=![]() ∠AFE=35°.
∠AFE=35°.
∵CD∥EF,
∴∠C=∠CFE=35°;
(2)∵AB∥CD,
∴∠DGF=∠A.
∵∠DGF是△GCF的外角,
∴∠DGF=∠C+∠AFC,
∴∠A=∠C+∠AFC.

练习册系列答案
相关题目