题目内容
【题目】已知二次函数图象的顶点坐标为M(1,0),直线![]() 与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在
与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在![]() 轴上.
轴上.

(1)求m的值及这个二次函数的解析式;
(2)若P(![]() ,0) 是
,0) 是![]() 轴上的一个动点,过P作
轴上的一个动点,过P作![]() 轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
①当0<![]() < 3时,求线段DE的最大值;
< 3时,求线段DE的最大值;
②若直线AB与抛物线的对称轴交点为N,问是否存在一点P,使以M、N、D、E为顶点的四边形是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
【答案】(1) ![]() ;
;![]() (2)①
(2)①![]() 有最大值
有最大值![]() ②存在.(2,0)(
②存在.(2,0)(![]() ,0)(
,0)(![]() ,0).
,0).
【解析】
(1)将A点坐标分别代入抛物线的直线,便可求出抛物线的解析式和m的值;
(2)过A作AH⊥PM于H,利用△MAB的面积=S梯形BOHA-S△BOM-S△AMH计算即可;
(3)①线段DE的长为h,根据P点坐标分别求出DE两点坐标,便可求出h与a之间的函数关系式,进而可求出线段DE的最大值;
②存在一点P,使以M、N、D、E为顶点的四边形是平行四边形,要使四边形NMED是平行四边形,必须DE=MN=2,由①知DE=|-a2+3a|,进而求出a的值,所以P的坐标可求出.
(1)设抛物线的解析式为y=a(x-1)2,
∵点A(3,4)在抛物线上,则4=a(3-1)2,
解得a=1,
∴抛物线的解析式为y=(x-1)2
∵点A(3,4)也在直线y=x+m,即4=3+m,
解得m=1;
(2)过A作AH⊥PM于H,
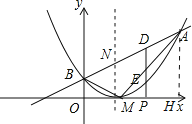
∵B(0,1),M(1,0),A(3,4),
∴OB=1,OH=3,AH=4,
∴△MAB的面积=S梯形BOHA-S△BOM-S△AMH=7.5-![]() ×1×1-
×1×1-![]() ×2×4=3;
×2×4=3;
(3)①已知P点坐标为P(a,0),则E点坐标为E(a,a2-2a+1),D点坐标为D(a,a+1),
h=DE=yD-yE=a+1-(a2-2a+1)=-a2+3a,
∴h与a之间的函数关系式为h=-a2+3a=-(a-![]() )2+
)2+![]() (0<a<3),
(0<a<3),
∴线段DE的最大值是![]() ;
;
②存在一点P,使以M、N、D、E为顶点的四边形是平行四边形,
理由是∵M(1,0),
∴把x=1代入y=x+1得:y=2,
即N(1,2),
∴MN=2,
要使四边形NMED是平行四边形,必须DE=MN=2,
由①知DE=|-a2+3a|,
∴2=|-a2+3a|,
解得:a1=2,a2=1,a3=![]() ,a4=
,a4=![]() ,
,
∴(2,0),(1,0)(因为和M重合,舍去)(![]() ,0),(
,0),(![]() ,0)
,0)
∴P的坐标是(2,0),(![]() ,0),(
,0),(![]() ,0).
,0).

 阅读快车系列答案
阅读快车系列答案