题目内容
【题目】已知在平面直角坐标系xOy中,抛物线![]() (b为常数)的对称轴是直线x=1.
(b为常数)的对称轴是直线x=1.
(1)求该抛物线的表达式;
(2)点A(8,m)在该抛物线上,它关于该抛物线对称轴对称的点为A',求点A'的坐标;
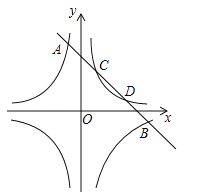
(3)选取适当的数据填入下表,并在如图5所示的平面直角坐标系内描点,画出该抛物线.

【答案】(1)![]() ;(2)(-6,49);(3)答案见解析.
;(2)(-6,49);(3)答案见解析.
【解析】
(1)由对称轴为![]() ,即可求出b的值,然后代入即可;
,即可求出b的值,然后代入即可;
(2)把![]() 代入解析式,求出m,利用抛物线的对称轴性质,即可得到点
代入解析式,求出m,利用抛物线的对称轴性质,即可得到点![]() 坐标;
坐标;
(3)选取对称轴左右两边的几个整数,计算出函数值,然后画出抛物线即可.
解:(1)∵对称轴为![]() ,
,
∴![]() .
.
∴![]() ;
;
∴抛物线的表达式为![]() .
.
(2)∵点A(8,m)在该抛物线的图像上,
∴当x=8时,![]() .
.
∴点A(8,49).
∴ 点A(8,49)关于对称轴对称的点A'的坐标为(-6,49).
(3)列表,如下:
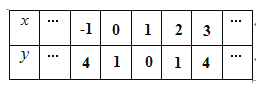
抛物线图像如下图:
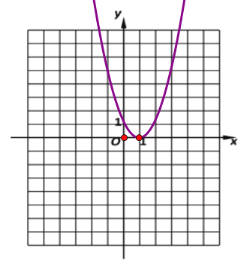

练习册系列答案
相关题目
【题目】甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7;
乙:5,7,8,7,8,9,7,9,10,10;
丙:7,6,8,5,4,7,6,3,9,5.
(1)根据以上数据完成下表:
平均数 | 中位数 | 方差 | |
甲 | 8 | 8 | |
乙 | 8 | 8 | 2.2 |
丙 | 6 | 3 |
(2)依据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定.求甲、乙相邻出场的概率.