Question

【题目】问题提出

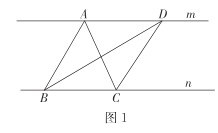
（1）如图1，的边BC在直线n上，过顶点A作直线m∥n，在直线m上任取一点D连接BD,CD，则的面积_______的面积（填“等于”大于”或“小于”）

问题探究

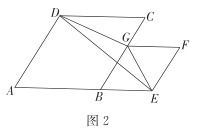
（2）如图2，在菱形ABCD和菱形BGFE中，，求的面积.

问题解决

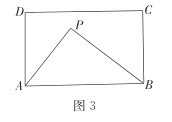
（3）如图3在矩形ABCD中，，在矩形ABCD内（可以在边上）存在点P，使得的面积等于矩形ABCD的面积的，求周长的最小值.

Answer 1

【答案】（1）等于；（2）的面积是；（3）周长的最小值是32.

【解析】

（1）两条平行线间的距离一定，那么△ABC与△ABD同底等高，所以面积相等；

（2）连接BD，根据已知条件和菱形的性质可得，由（1）可得，

求出等边三角形BGE即可得出答案；

（3）过点P作，交DA于点F，交BC于点G，作点B关于FG的对称点B'，连接，根据两点之间线段最短得出从而得出，再根据的面积等于矩形ABCD的面积的，得出BG的长，

继而求出的长，即可得出答案；

（1）∵m∥n，

∴和同底等高；

∴的面积=的面积

故答案为：等于；

（2）如图1，连接BD，过点B作于点H.

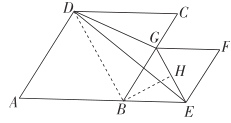
∴四边形ABCD和四边形BEFG是菱形，，

，

，

是等边三角形，

∴，

在中，，

的面积是

（3）如图2，过点P作，交DA于点F，交BC于点G，作点B关于FG的对称点B'，连接.

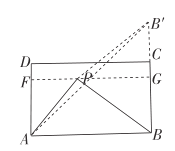
的面积是矩形ABCD的面积的，

∴P是FG上的一动点

∵点B与B’关于FG对称，

，

即

的面积是矩形ABCD的面积的，

边AB边上的高是8，

.

在中，，

.

综上，周长的最小值是32.