题目内容
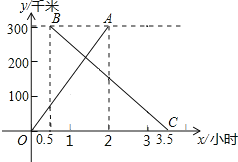
【题目】已知,建立如图所示的直角坐标系,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识:
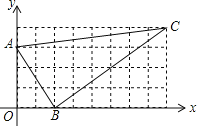
(1)求出△ABC的面积;
(2)判断△ABC是什么形状?并说明理由;
(3)求直线AC的函数表达式.
【答案】(1)13;(2)△ABC是直角三角形.(3)y=![]() x+3.
x+3.
【解析】
试题分析:(1)用长方形的面积减去三个小三角形的面积即可求出△ABC的面积.
(2)根据勾股定理求得△ABC各边的长,再利用勾股定理的逆定理进行判定,从而不难得到其形状.
(3)设直线AC的函数表达式为y=kx+b,把A(0,3),C(8,4)代入得出方程组,解方程组即可.
解:(1)△ABC的面积=4×8﹣1×8÷2﹣2×3÷2﹣6×4÷2=13.
故△ABC的面积为13;
(2)△ABC是直角三角形;理由如下:
∵正方形小方格边长为1
∴AC=![]() =
=![]() ,AB=
,AB=![]() =
=![]() ,BC=
,BC=![]() =2
=2![]() ,
,
∵在△ABC中,AB2+BC2=13+52=65,AC2=65,
∴AB2+BC2=AC2,
∴△ABC是直角三角形.
(3)设直线AC的函数表达式为y=kx+b,
把A(0,3),C(8,4)代入得:![]() ,
,
解得:![]() ,
,
∴直线AC的函数表达式为y=![]() x+3.
x+3.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
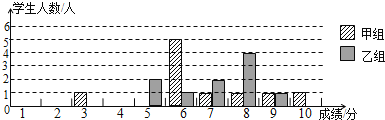
天天向上课时同步训练系列答案【题目】某校团委举办了一次“中国梦,我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达6分以上为合格,达到9分以上(含9分)为优秀.这次竞赛中甲、乙两组学生成绩分布的条形统计图如下.
(1)补充完成下列的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲 | 6.7 |
| 3.41 | 90% | 20% |
乙 |
| 7.5 |
| 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.