题目内容
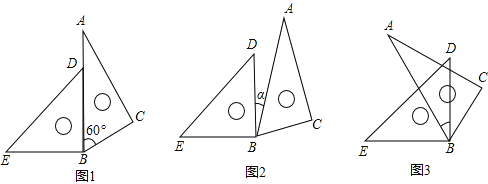
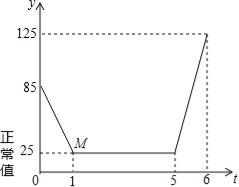
【题目】近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.随着空气变化的图象(如图),请根据图象,解答下列问题:
(1)写出题中的变量;
(2)写出点M的实际意义;
(3)求第1小时内,y与t的一次函数表达式;
(4)已知第5﹣6小时是小强妈妈做晚餐的时间,厨房内油烟导致PM2.5浓度升高.若该净化器吸收PM2.5的速度始终不变,则第6小时之后,预计经过多长时间室内PM2.5浓度可恢复正常?
【答案】(1)时间t和PM2.5的浓度;(2)1小时后PM2.5的浓度达到正常值25;(3)y=﹣60t+85;(4)预计经过![]() 时间室内PM2.5浓度可恢复正常.
时间室内PM2.5浓度可恢复正常.
【解析】试题分析:(1)由函数图象可以得出变量是时间t和PM2.5的浓度;
(2)1小时后PM2.5的浓度达到正常值25;
(3)设第1小时内,y与t的一次函数表达式为y=kt+b,由待定系数法求出其解即可;
(4)设经过a小时后室内PM2.5浓度可恢复正常,由工程问题的数量关系建立方程求出其解即可.
解:(1)由函数图象,得
题中的变量是时间t和PM2.5的浓度;
(2)点M的实际意义是:
1小时后PM2.5的浓度达到正常值25;
(3)设第1小时内,y与t的一次函数表达式为y=kt+b,由题意,得
![]() ,
,
解得:![]() ,
,
∴y=﹣60t+85;
(4)设经过a小时后室内PM2.5浓度可恢复正常,由题意,得
125﹣60a=25,
解得:a=![]() .
.
答:预计经过![]() 时间室内PM2.5浓度可恢复正常.
时间室内PM2.5浓度可恢复正常.

【题目】已知,建立如图所示的直角坐标系,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识:
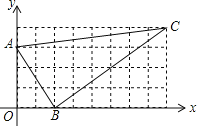
(1)求出△ABC的面积;
(2)判断△ABC是什么形状?并说明理由;
(3)求直线AC的函数表达式.
【题目】学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如表:
选手 | 表达能力 | 阅读理解 | 综合素质 | 汉字听写 |
甲 | 85 | 78 | 85 | 73 |
乙 | 73 | 80 | 82 | 83 |
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.