题目内容
【题目】定义正整数m，n的运算：m△n=
+
+
+
+…+
（1）计算3△2的值为 ；运算“△”满足交换规律吗？回答： （填“是”或“否”）
（2）探究：计算2△10=
+
+
+
+…+
的值．
为解决上面的问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系的几何图形结合起来，最终解决问题．
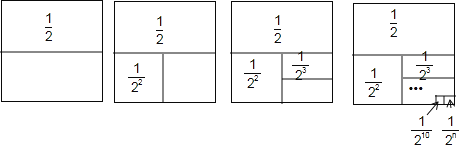
如图所示，第一次分割，把正方形的面积二等分，其中阴影部分的面积为
；
第2此分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为
；
第3次分割，把上次分割图中空白部分的面积继续二等分，…；依此类推，…
第10次分割，把二次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为﹣
++…+
，最后空白部分的面积是；根据第10次分割图可以得出计算结果：
+
+
+
+…+
=1﹣．
进一步分析可得出，++++…+
=
（3）已知n是正整数，计算4△n=
+
﹣
+
﹣…+
的结果．
按指定方法解决问题：请仿照以上做法，只需画出第n次分割图并作标注，写出最终结果的推理步骤；或借用以上结论进行推理，写出必要的步骤．
【答案】（1）
；否；（2）1﹣
；（3）
﹣
．
【解析】
试题分析：（1）根据新定义运算法则进行计算即可；
（2）根据计算2△10=
+
+
+
+…+
的值的计算过程得到规律解题；
（3）根据探究的分割方法依次进行分割，然后表示出阴影部分的面积，再除以3即可．
解：（1）3△2=
+
=．
而2△3=
+
+=
，
则3△2≠2△3，
所以运算“△”不满足交换规律．
故答案是：；否；
（2）如图所示，第一次分割，把正方形的面积二等分，其中阴影部分的面积为
；
第2此分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为
；
第3次分割，把上次分割图中空白部分的面积继续二等分，…；依此类推，…
第10次分割，把二次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为﹣
+
+…+
，最后空白部分的面积是；
根据第10次分割图可以得出计算结果：++
+
+…+
=1﹣．
进一步分析可得出，
+
+++…+
=1﹣．
故答案是：1﹣．
（3）第1次分割，把正方形的面积四等分，
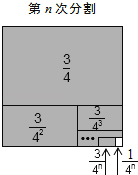
其中阴影部分的面积为
；
第2次分割，把上次分割图中空白部分的面积继续四等分，
阴影部分的面积之和为；
第3次分割，把上次分割图中空白部分的面积继续四等分，
…，
第n次分割，把上次分割图中空白部分的面积最后四等分，
所有阴影部分的面积之和为：+
+
+…+
，
最后的空白部分的面积是
，
根据第n次分割图可得等式：+
+
+…+
=1﹣
，
两边同除以3，得
+
+
+…+=﹣．
【题目】某车间20名工人日加工零件数如下表所示：
日加工零件数 | 4 | 5 | 6 | 7 | 8 |
人数 | 2 | 6 | 5 | 4 | 3 |
这些工人日加工零件数的众数、中位数、平均数分别是（ ）
A．5、6、5 B．5、5、6 C．6、5、6 D．5、6、6
