Question

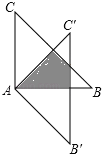
【题目】如图，△ABC绕点A顺时针旋转45°得到△AB′C′，若∠BAC=90°，AB=AC=2，则图中阴影部分的面积等于 ．

Answer 1

【答案】4﹣4．

【解析】

试题分析：根据等腰直角三角形的性质得∠B=∠C=45°，再根据旋转的性质得∠CAC′=∠BAB′=45°，∠B′=∠B=45°，AB′=AB=2，于是可判断△AFB′是等腰直角三角形，得到AD⊥BC，B′F⊥AF，AF=AB′=2，可计算出BF=AB﹣AF=2﹣2，接着证明△ADB和△BEF为等腰直角三角形得到AD=BD=AB=2，EF=BF=2﹣2，然后利用图中阴影部分的面积=S△ADB﹣S△BEF进行计算即可．

解：如图，

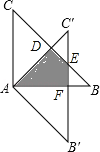
∵∠BAC=90°，AB=AC=2，

∴∠B=∠C=45°，

∵△ABC绕点A顺时针旋转45°得到△AB′C′，

∴∠CAC′=∠BAB′=45°，∠B′=∠B=45°，AB′=AB=2，

∴△AFB′是等腰直角三角形，

∴AD⊥BC，B′F⊥AF，AF=AB′=2，

∴BF=AB﹣AF=2﹣2，

∵∠B=45°，EF⊥BF，AD⊥BD，

∴△ADB和△BEF为等腰直角三角形，

∴AD=BD=AB=2，EF=BF=2﹣2，

∴图中阴影部分的面积=S△ADB﹣S△BEF

=22﹣（2﹣2）2

=4﹣4．

故答案为4﹣4．