题目内容
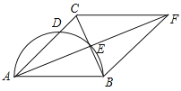
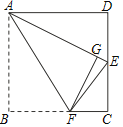
【题目】如图,在正方形纸片ABCD中,E是CD的中点,将正方形纸片折叠,点B落在线段AE上的点G处,折痕为AF.若AD=2,则BF的长为_____.
【答案】![]() ﹣1
﹣1
【解析】
设BF=x,则FG=x,CF=2﹣x,在Rt△GEF中,利用勾股定理可得EF2=![]() ,在Rt△FCE中,利用勾股定理可得EF2=(2﹣x)2+12,从而得到关于x的方程,求解x即可.
,在Rt△FCE中,利用勾股定理可得EF2=(2﹣x)2+12,从而得到关于x的方程,求解x即可.
解:设BF=x,则FG=x,CF=2﹣x.
在Rt△ADE中,利用勾股定理可得AE=![]() .
.
根据折叠的性质可知AG=AB=2,所以GE=![]() ﹣2.
﹣2.
在Rt△GEF中,利用勾股定理可得EF2=(![]() ﹣2)2+x2,
﹣2)2+x2,
在Rt△FCE中,利用勾股定理可得EF2=(2﹣x)2+12,
所以(![]() ﹣2)2+x2=(2﹣x)2+12,
﹣2)2+x2=(2﹣x)2+12,
解得x=![]() ﹣1,
﹣1,
∴BF=![]() ﹣1,
﹣1,
故答案为:![]() ﹣1.
﹣1.

练习册系列答案
相关题目
【题目】已知二次函数![]() 自变量
自变量![]() 的值和它对应的函数值
的值和它对应的函数值![]() 如下表所示:
如下表所示:
| … | 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | … |
(1)点M是该二次函数图象上一点,若点M纵坐标为8时,求点M的坐标;
(2)设该二次函数图象与![]() 轴的左交点为
轴的左交点为![]() ,它的顶点为
,它的顶点为![]() ,该图象上点
,该图象上点![]() 的横坐标为4,求
的横坐标为4,求![]() 的面积.
的面积.