题目内容
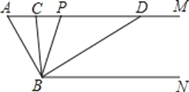
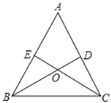
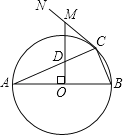
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.
(1)求证:MD=MC;
(2)若⊙O的半径为5,AC=4![]() ,求MC的长.
,求MC的长.
【答案】(1)证明见解析;(2)MC=![]() .
.
【解析】(1)连接OC,利用切线的性质证明即可;
(2)根据相似三角形的判定和性质以及勾股定理解答即可.
(1)连接OC,

∵CN为⊙O的切线,
∴OC⊥CM,∠OCA+∠ACM=90°,
∵OM⊥AB,
∴∠OAC+∠ODA=90°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠ACM=∠ODA=∠CDM,
∴MD=MC;
(2)由题意可知AB=5×2=10,AC=4![]() ,
,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴BC=![]() =2
=2![]() ,
,
∵∠AOD=∠ACB,∠A=∠A,
∴△AOD∽△ACB,
∴![]() ,即
,即![]() ,
,
可得:OD=2.5,
设MC=MD=x,在Rt△OCM中,由勾股定理得:(x+2.5)2=x2+52,
解得:x=![]() ,
,
即MC=![]() .
.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
【题目】某学习小组在学习了函数及函数图象的知识后,想利用此知识来探究周长一定的矩形其边长分别为多少时面积最大. 请将他们的探究过程补充完整.
(1)列函数表达式:若矩形的周长为8,设矩形的一边长为x,面积为y,则有y=____________;
(2)上述函数表达式中,自变量x的取值范围是____________;
(3)列表:
x | … | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
y | … | 1.75 | 3 | 3.75 | 4 | 3.75 | 3 | m | … |
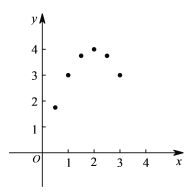
写出m=____________;
(4)画图:在平面直角坐标系中已描出了上表中部分各对应值为坐标的点,请你画出该函数的图象;
(5)结合图象可得,x=____________时,矩形的面积最大;写出该函数的其它性质(一条即可):____________.