Question

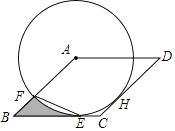
【题目】如图，已知⊙A与菱形ABCD的边BC相切于点E，与边AB相交于点F，连接EF．

（1）求证：CD是⊙A的切线；

（2）若⊙A的半径为2，tan∠BEF＝，求图中阴影部分的面积．

Answer 1

【答案】（1）详见解析；（2）

【解析】

（1）作AH⊥CD于H，连结AE，AC， 根据菱形性质得到AC平分∠BCD，AE⊥BC，AH⊥CD，得到AE＝AH，即CD为⊙A的半径，所以⊙A与边CD也相切；（2）tan∠BEF＝，所以∠BEF＝30°，得到∠AEF＝60°，又因为AE＝AF，得到∠FAE＝60°，∠B＝30°，然后利用扇形公式算出扇形FAE面积，用三角形ABE的面积减去扇形AEF面积即可

（1）证明：作AH⊥CD于H，连结AE，AC，如图，

∵BC与⊙A相切于点E，

∴AE⊥BC，

∵四边形ABCD为菱形，

∴AC平分∠BCD，

而AE⊥BC，AH⊥CD，

∴AE＝AH，

即CD为⊙A的半径，

∴⊙A与边CD也相切；

（2）解：∵tan∠BEF＝，

∴∠BEF＝30°，

∵∠AEB＝90°，

∴∠AEF＝60°，

∵AE＝AF，

∴∠FAE＝60°，∠B＝30°，

∵AE＝2，

∴S扇形FAE＝，BE＝

∴S阴影＝S△ABE﹣S扇形AEF＝×2×2﹣π＝2﹣π．