题目内容
【题目】把四块长为a,宽为b的长方形木板围成如图所示的正方形,请解答下列问题:
(1)按要求用含a,b的式子表示空心部分的正方形的面积S(结果不要化简,保留原式):
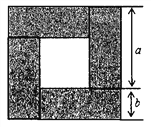
①用大正方形面积减去四块木板的面积表示:S= ;
②直接用空心部分的正方形边长的平方表示:S= ;
(2)由①、②可得等式 ;
(3)用整式的乘法验证(2)中的等式成立.
【答案】(1)① ![]() ; ②
; ②![]() (2)
(2) ![]() ;(3)答案见解析
;(3)答案见解析
【解析】试题分析: (1)①观察图形,可得图中大正方形的边长为a+b,每一块长方形木板的长为a,宽为b,根据正方形的面积=边长的平方,长方形的面积=长×宽即可求解;
②观察图形,可得图中空心部分的正方形边长为a-b,根据正方形的面积=边长的平方即可求解;(2)根据空心部分的正方形的面积不变即可得到等式;
(3)利用完全平方公式证明即可.
②![]()
(2)![]()
(3) 验证: 左边 = ![]()
= ![]()
= ![]()
= ![]()
∵ 左边 = 右边
∴ (2)中的等式成立
点睛:此题考查完全平方公式的几何背景,利用面积、边的关系建立等量关系是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前6名选手的得分如下:
序号 项目 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩/分 | 85 | 92 | 84 | 90 | 84 | 80 |
面试成绩/分 | 90 | 88 | 86 | 90 | 80 | 85 |
根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分).
(1)这6名选手笔试成绩的中位数是________分,众数是________分;
(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(3)求出其余五名选手的综合成绩,并以综合成绩排序确定前两名人选.