题目内容
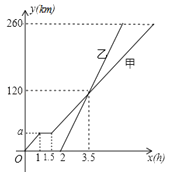
【题目】甲、乙两车从A地驶向B地，甲车比乙车早行驶2h，并且在途中休息了0.5h，休息前后速度相同，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．
（1）求出图中a的值；
（2）求出甲车行驶路程y（km）与时间x（h）的函数表达式，并写出相应的x的取值范围；
（3）当甲车行驶多长时间时，两车恰好相距40km．
【答案】（1）40；（2）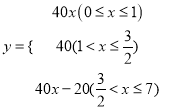
；（3）行驶1小时或（1-1.5）小时或2.5小时或4.5小时，两车恰好相距40km.
【解析】试题分析：（1）求出甲的速度，根据休息前后速度相同和距离等于速度乘时间求出a的值；
（2）根据图象中自变量的取值范围分别求出各段的函数表达式；
（3）分别从甲在乙前和甲在乙后两种情况列出方程，求出时间．
试题解析：解：（1）由题意120÷（3.5﹣0.5）=40，a=1×40=40；
（2）①当0≤x≤1时，设y与x之间的函数关系式为y=k1x，把（1，40）代入，得k1=40
∴y=40x；
②当1＜x≤
时，y=40；
③当
＜x≤7时，设y与x之间的函数关系式为y=k2x+b，由题意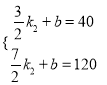，得： 
，解得： 
，∴y=40x﹣20；
综上所述：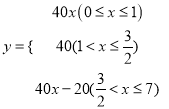 
；
（3）设乙车行驶的路程y与时间x之间的解析式为y=mx+n，由题意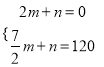，得： 
，解得： 
，∴y=80x﹣160，当40x﹣20﹣（80x﹣160）=40时，解得：x=2.5．
当80x﹣160﹣（40x﹣20）=40时，解得：x=4.5．
答：甲车行驶1小时（或1﹣1.5小时）或2.5小时或4.5小时，两车恰好相距40km．
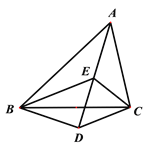
阅读快车系列答案
【题目】如图，均匀的正四面体的各面依次标有1，2，3，4四个数字.小明做了60次投掷试验，结果统计如下：
朝下数字 | 1 | 2 | 3 | 4 |
出现的次数 | 16 | 20 | 14 | 10 |
【1】计算上述试验中“4朝下”的频率是_________
【2】根据试验结果，投掷一次正四面体，出现2朝下的概率是
.”的说法正确吗？为什么？
【3】随机投掷正四面体两次，请用列表或画树状图法，求两次朝下的数字之和大于4的概率．
