题目内容
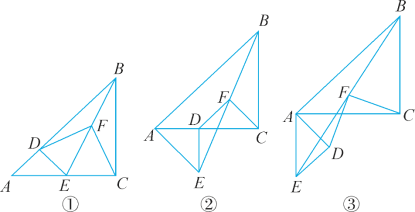
【题目】已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,F为BE的中点,连结DF,CF.
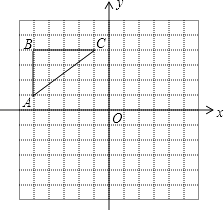
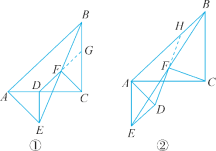
(1)如图①,当点D在AB上,点E在AC上,请直接写出此时线段DF,CF的数量关系和位置关系.
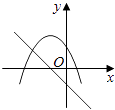
(2)如图②,在(1)的条件下将△ADE绕点A顺时针旋转45°,请你判断此时(1)中的结论是否仍然成立,并证明你的判断.
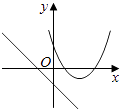
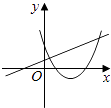
(3)如图③,在(1)的条件下将△ADE绕点A顺时针旋转90°,若AD=1,AC=![]() ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果).
【答案】(1) DF=CF,DF⊥CF;(2)(1)中的结论仍然成立,证明见解析;(3)CF=![]() .
.
【解析】
(1)根据“直角三角形斜边上的中线等于斜边的一半”可知DF=CF,根据∠DFE=2∠DBF,∠CFE=2∠CBF,得到∠EFD+∠EFC=2∠ABC=90°,DF⊥CF.
(2)延长DF交BC于点G,先证明△DEF≌△GBF,得到DE=GB,DF=GF,根据AD=DE,AB=BC,得到DC=GC又因为∠ACB=90°,所以DF=CF且DF⊥CF.
(3)延长DF交BA于点H,先证明△DEF≌△HBF,得到DE=BH,根据旋转条件可以△ADH为直角三角形,由△ABC和△ADE是等腰直角三角形,AC=2![]() ,可以求出AB的值,进而可以根据勾股定理可以求出DH,再求出DF,求出得CF的值.
,可以求出AB的值,进而可以根据勾股定理可以求出DH,再求出DF,求出得CF的值.
(1) DF=CF. DF⊥CF.
(2)(1)中的结论仍然成立.证明如下:
如解图①,延长DF交BC于点G.
∵∠ADE=∠ACB=90°,∴DE∥BC,
∴∠DEF=∠GBF,∠EDF=∠BGF.
∵F为BE的中点,∴EF=BF,
∴△DEF≌△GBF(AAS),
∴DE=GB,DF=GF.
∵AD=DE,∴AD=GB.
∵AC=BC,∴AC-AD=BC-GB,即DC=GC.
∵∠ACB=90°,∴△DCG是等腰直角三角形.
∵DF=GF,∴DF=CF,DF⊥CF.
(3)CF=![]() .
.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案