题目内容
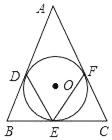
【题目】在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
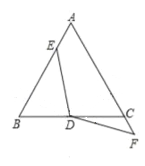
(1)如图,若DF⊥AC,垂足为F,证明:DE=DF
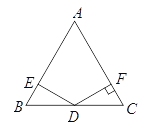
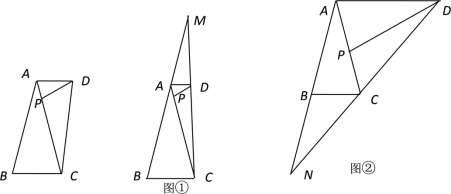
(2)如图,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.DE=DF仍然成立吗?说明理由。
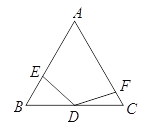
(3)将∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线相交于点F,DE=DF仍然成立吗? 直接说出结论,不必说明理由。
【答案】(1)证明见解析(2)成立 (3)成立
【解析】
(1)证明△ABC是等边三角形,得∠B=∠C,BD=CD,进而证明△BED≌△CFD(ASA),即可证明DE=DF.
(2)取AC中点G,连接DG,证明△EDG≌△FDC(ASA),即可证明结论仍成立.
(3)过点D作DN⊥AC于N,DM⊥AB于M,得∠NDF=∠MDE,证明△DME≌△DNF(ASA)即可证明结论仍成立.
解:(1)∵AB=AC,∠A=60°,
∴△ABC是等边三角形,即∠B=∠C=60°,
∵D是BC的中点,
∴BD=CD,
∵∠EDF=120°,DF⊥AC,
∴∠FDC=30°,
∴∠EDB=30°,
∴△BED≌△CFD(ASA),
∴DE=DF.
(2)取AC中点G,连接DG,如下图,
∵D为BC的中点,
∴DG=![]() AC=BD=CD,
AC=BD=CD,
∴△BDG是等边三角形,
∴∠GDE+∠EDB=60°,
∵∠EDF=120°,
∴∠FDC+∠EDB=60°,
∴∠EDG=∠FDC,
∴△EDG≌△FDC(ASA),
∴DE=DF.
∴结论仍然成立.
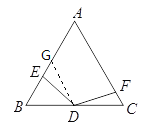
(3)如下图,过点D作DN⊥AC于N,DM⊥AB于M,
∴∠DME=∠DNF=90°,
由(1)可知∠B=∠C=60°,
∴∠NDC=∠BDM=30°,DM=DN,
∴∠MDN=120°,即∠NDF=∠MDE,
∴△DME≌△DNF(ASA),
∴DE=DF,
∴仍然成立.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案