ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌЮЊСЫУРЛЏЛЗОГЃЌНЈЩшїШСІКєКЭКЦЬиЃЌКєКЭКЦЬиЪазМБИдквЛИіЙуГЁЩЯжжжВМзЁЂввСНжжЛЈЛмОЪаГЁЕїВщЃЌМзжжЛЈЛмЕФжжжВЗбгУ![]() ЃЈдЊЃЉгыжжжВУцЛ§
ЃЈдЊЃЉгыжжжВУцЛ§![]() жЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОввжжЛЈЛмЕФжжжВЗбгУЮЊУПЦНЗНУз100дЊ
жЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОввжжЛЈЛмЕФжжжВЗбгУЮЊУПЦНЗНУз100дЊ
ЃЈ1ЃЉжБНгаДГіЕБ![]() КЭ
КЭ![]() ЪБЃЌ
ЪБЃЌ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЎ
ЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ2ЃЉЙуГЁЩЯМзЁЂввСНжжЛЈЛмЕФжжжВУцЛ§ЙВ![]() ЃЌШєМзжжЛЈЛмЕФжжжВУцЛ§ВЛЩйгк
ЃЌШєМзжжЛЈЛмЕФжжжВУцЛ§ВЛЩйгк![]() ЃЌЧвВЛГЌЙ§ввжжЛЈЛмжжжВУцЛ§ЕФ2БЖЃЌФЧУДгІИУдѕбљЗжХфМзЁЂввСНжжЛЈЛмЕФжжжВУцЛ§ВХФмЪЙжжжВзмЗбгУзюЩйЃПзюЩйзмЗбгУЮЊЖрЩйдЊЃП
ЃЌЧвВЛГЌЙ§ввжжЛЈЛмжжжВУцЛ§ЕФ2БЖЃЌФЧУДгІИУдѕбљЗжХфМзЁЂввСНжжЛЈЛмЕФжжжВУцЛ§ВХФмЪЙжжжВзмЗбгУзюЩйЃПзюЩйзмЗбгУЮЊЖрЩйдЊЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉгІИУЗжХфМзЁЂввСНжжЛЈЛмЕФжжжВУцЛ§ЗжБ№ЪЧ800m2КЭ400m2ЃЌВХФмЪЙжжжВзмЗбгУзюЩйЃЌзюЩйзмЗбгУЮЊ121000дЊЃЎ
ЃЛЃЈ2ЃЉгІИУЗжХфМзЁЂввСНжжЛЈЛмЕФжжжВУцЛ§ЗжБ№ЪЧ800m2КЭ400m2ЃЌВХФмЪЙжжжВзмЗбгУзюЩйЃЌзюЩйзмЗбгУЮЊ121000дЊЃЎ
ЁОНтЮіЁП
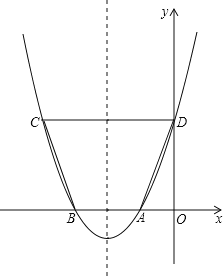
ЃЈ1ЃЉгЩЭМПЩжЊyгыxЕФКЏЪ§ЙиЯЕЪНЪЧЗжЖЮКЏЪ§ЃЌД§ЖЈЯЕЪ§ЗЈЧѓНтЮіЪНМДПЩЃЎ
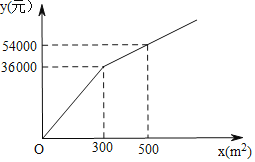
ЃЈ2ЃЉЩшжжжВзмЗбгУЮЊWдЊЃЌМзжжЛЈЛмжжжВЮЊam2ЃЌдђввжжЛЈЛмжжжВЃЈ1200aЃЉm2ЃЌИљОнЪЕМЪвтвхПЩвдШЗЖЈaЕФЗЖЮЇЃЌНсКЯжжжВЗбгУyЃЈдЊЃЉгыжжжВУцЛ§xЃЈm2ЃЉжЎМфЕФКЏЪ§ЙиЯЕПЩвдЗжРрЬжТлзюЩйЗбгУЮЊЖрЩйЃЎ
НтЃКЃЈ1ЃЉЕБ0ЁмxЁм300ЃЌЩшy=kxЃЌНЋЕуЃЈ300,36000ЃЉДњШыЕУЃК
36000=300kЃЌ
Ёрk=120ЃЌ
ЕБxЃО300ЃЌЩшy=mx+nЃЌНЋЕуЃЈ300,36000ЃЉМАЕуЃЈ500,54000ЃЉДњШы
ЕУ![]() ЃЌНтЕУm=90ЃЌn=9000ЃЌ
ЃЌНтЕУm=90ЃЌn=9000ЃЌ
Ёрy=90x+9000ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЃЈ2ЃЉЩшжжжВзмЗбгУЮЊWдЊЃЌМзжжЛЈЛмжжжВЮЊam2ЃЌдђввжжЛЈЛмжжжВЃЈ1200aЃЉm2ЃЌ
гЩЬтвтЕУЃК![]() ЃЌ
ЃЌ
Ёр200ЁмaЁм800
ЕБ200ЁмaЁм300ЪБЃЌW1ЃН120aЃЋ100ЃЈ1200aЃЉЃН20aЃЋ120000ЃЎ
Ёп20ЃО0ЃЌW1ЫцaдіДѓЖјдіДѓЃЌ
ЁрЕБaЃН200ЪБЃЎWminЃН124000дЊ
ЕБ300ЃМaЁм800ЪБЃЌW2ЃН90aЃЋ9000ЃЋ100ЃЈ1200aЃЉЃН10a +129000ЃЎ
Ёп-10ЃМ0ЃЌW2ЫцaдіДѓЖјМѕаЁЃЌ
ЕБaЃН800ЪБЃЌWminЃН121000дЊ
Ёп124000ЃО121000
ЁрЕБaЃН800ЪБЃЌзмЗбгУзюЩйЃЌзюЩйзмЗбгУЮЊ121000дЊЃЎ
ДЫЪБввжжЛЈЛмжжжВУцЛ§ЮЊ1200800ЃН400ЃЈm2ЃЉЃЎ
Д№ЃКгІИУЗжХфМзЁЂввСНжжЛЈЛмЕФжжжВУцЛ§ЗжБ№ЪЧ800m2КЭ400m2ЃЌВХФмЪЙжжжВзмЗбгУзюЩйЃЌзюЩйзмЗбгУЮЊ121000дЊЃЎ

 дФЖСПьГЕЯЕСаД№АИ
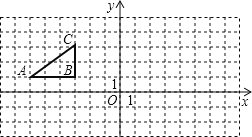
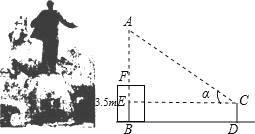
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПХЉАЫЪІЪЏКгзгЪаФГжабЇГѕШ§ЃЈ1ЃЉАрЕФбЇЩњЃЌдквЛДЮЪ§бЇЛюЖЏПЮжаЃЌРДЕНЪагЮэЌЙуГЁЃЌВтСПзјТфдкЙуГЁжааФЕФЭѕе№НЋОќЕФЭЯёИпЖШЃЌвбжЊЭЯёЕззљЕФИпЮЊ3.5mЃЎФГаЁзщЕФЪЕЯАБЈИцШчЯТЃЎЧыФуМЦЫуГіЭЯёЕФИпЃЈНсЙћОЋШЗЕН0.1mЃЉ
ЪЕЯАБЈИц2003Фъ9дТ25Ше
ЬтФП1 | ВтСПЕзВППЩвдЕНДяЕФЭЯёИп | |||
| ||||
Вт ЕУ Ъ§ Он | ВтСПЯюФП | ЕквЛДЮ | ЕкЖўДЮ | ЦНОљжЕ |
BDЕФГЄ | 12.3m | 11.7m | ||
ВтЧуЦїCDЕФИп | 1.32m | 1.28m | ||
ЧуаБНЧ | ІС=30Ёу56' | ІС=31Ёу4' | ||
МЦ Ыу | ||||
НсЙћ | ||||
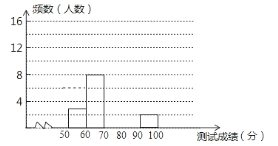
ЁОЬтФПЁПЮЊСЫдіЧПбЇЩњЛЗБЃвтЪЖЃЌЮвЧјОйАьСЫЪзНьЁАЛЗБЃжЊЪЖДѓШќЁБЃЌОбЁАЮКѓга30УћбЇЩњВЮМгОіШќЃЌет30ЃЌУћбЇЩњЭЌЪТНтД№50ИібЁдёЬтЃЌШєУПе§ШЗвЛИібЁдёЬтЕУ2ЗжЃЌИљОнВтЪдГЩМЈЛцжЦГіВПЗжЦЕЪ§ЗжВМБэКЭВПЗжЦЕЪ§ЗжВМжБЗНЭМШчЭМБэЃК
зщБ№ | ГЩМЈxЗж | ЦЕЪ§ЃЈШЫЪ§ЃЉ |
Ек1зщ | 50ЁмxЃМ60 | 3 |
Ек2зщ | 60ЁмxЃМ70 | 8 |
Ек3зщ | 70ЁмxЃМ80 | 13 |
Ек4зщ | 80ЁмxЃМ90 | a |
Ек5зщ | 90ЁмxЃМ100 | 2 |
ЃЈ1ЃЉЧѓБэжаaЕФжЕЃЛ
ЃЈ2ЃЉЧыАбЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉШєВтЪдГЩМЈВЛЕЭгк80ЗжЮЊгХауЃЌдђБОДЮВтЪдЕФгХауТЪЪЧЖрЩйЃП
ЃЈ4ЃЉЕк4зщЕФЭЌбЇНЋГщГі3УћЖдЕквЛзщ3УћЭЌбЇНјааЁАвЛАявЛЁБИЈЕМЃЌдђЕк4зщЕФаЁгюгыаЁЧПФмЭЌЪБГщЕНЕФИХТЪЪЧЖрЩйЃП