题目内容
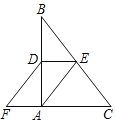
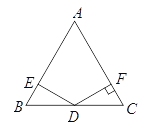
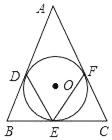
【题目】如图,△ABC的三边分别切⊙O于D,E,F.
(1)若∠A=40°,求∠DEF的度数;
(2)AB=AC=13,BC=10,求⊙O的半径.
【答案】(1)70°(2)![]()
【解析】
(1)连OD,OF;先利用三角形的内角和求出∠DOF,再根据圆周角定理求出角DEF.
(2)过A做AM⊥BC于M,求出BM=![]() BC,则S△ABC=60 ,设圆O的半径的半径是r,则
BC,则S△ABC=60 ,设圆O的半径的半径是r,则
![]() (13+13+10)r=60,求出r即可.
(13+13+10)r=60,求出r即可.
(1)连OD,OF,如图,
则OD⊥AB,OF⊥AC;
∴∠DOF=180°-∠A=180°-40°=140°,
又∵∠DEF=![]() ∠DOF=
∠DOF=![]() ×140°=70°,
×140°=70°,
(2)过A做AM⊥BC于M,
∵AB=AC
∴BM=![]() BC=
BC=![]() ×10=5,
×10=5,
则AM=12
则S△ABC=60 .
设圆O的半径的半径是r,则
![]() (13+13+10)r=60,
(13+13+10)r=60,
解得:r=![]() .
.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目