题目内容
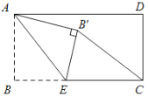
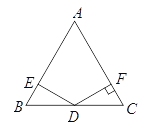
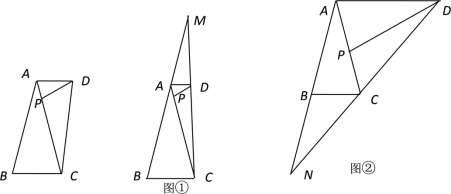
【题目】如图，在△ABC中，AB=AC=10，BC=5，点P是边AC上的一个动点，∠APD=∠ABC，AD∥BC，连接CD．
（1）求证AD=2AP；
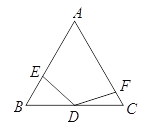
（2）如图①，若BA与CD的延长线交于点M，AP＝1，求AM的长；
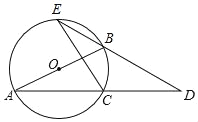
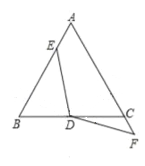
（3）如图②，若AB与DC的延长线交于点N，当△CDP与△BCN相似时，求证点P是AC的中点．
【答案】（1）见解析；（2）AM=
；（3）点P是AC的中点.
【解析】
(1)证明△DAP∽△ACB，得
，即可得解；
（2）证明△MAD∽△MBC，得
，即可得解；
（3）证明△NBC∽△NAD，得
，故
；由△CPD∽△CBN，得
，
，求解即可.
（1）证明：∵AD∥BC
∴∠DAP=∠ACB
又∵∠APD=∠ABC
∴△DAP∽△ACB
∴
∴
∴AD=2AP
（2）∵AP=1，∴AD=2AP=2
∵AD∥BC
∴△MAD∽△MBC
∴
∴
∴AM=
（3）∵∠APD=∠ABC
∴∠CPD=∠CBN
又∵∠ACP＞∠N
∴当△CDP与△BCN相似时，只能是△CPD∽△CBN
设AP=x，BN=y，则AD=PD=2x，CP=10－x
∵△CPD∽△CBN，∴，∴
∵AD∥BC，∴△NBC∽△NAD，∴，∴
解出x=5，∴点P是AC的中点.
练习册系列答案
阅读快车系列答案
相关题目
