题目内容
 在平面直角坐标系中给定以下五个点A(-3,0),B(-1,4),C(0,3),D(
在平面直角坐标系中给定以下五个点A(-3,0),B(-1,4),C(0,3),D(| 1 |
| 2 |
| 7 |
| 4 |
(1)请从五点中任选三点,求一条以平行于y轴的直线为对称轴的抛物线的解析式;
(2)求该抛物线的顶点坐标和对称轴,并画出草图;
(3)已知点F(-1,
| 15 |
| 4 |
| 17 |
| 4 |
| 17 |
| 4 |
| 17 |
| 4 |
| 1 |
| 2 |
| 7 |
| 4 |
| 17 |
| 4 |
分析:首先用待定系数法求得抛物线的解析式,利用抛物线的公式求得抛物线的顶点坐标及对称轴,构造直角三角形,利用勾股定理求得线段EF、DF的长,再与点E、D到直线y=
的距离比较,得到点E和点D分别到点F的距离等于各自到直线y=
的距离.
最后可猜想:以抛物线上任意一点P为圆心,以PF为半径的圆与直线y=
相切.
| 17 |
| 4 |
| 17 |
| 4 |
最后可猜想:以抛物线上任意一点P为圆心,以PF为半径的圆与直线y=
| 17 |
| 4 |
解答: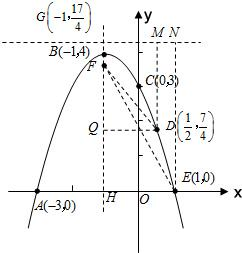 解:(1)设抛物线的解析式为y=ax2+bx+c,
解:(1)设抛物线的解析式为y=ax2+bx+c,
且过点A(-3,0),C(0,3),E(1,0),
由(0,3)在y=ax2+bx+cH.
则c=3.
得方程组
,
解得a=-1,b=-2.
∴抛物线的解析式为y=-x2-2x+3.
(2)由y=-x2-2x+3=-(x+1)2+4,
得顶点坐标为(-1,4),对称轴为x=-1.
(3)①连接EF,过点E作直线y=
的垂线,垂足为N,
则EN=HG=
.
在Rt△FHE中,HE=2,HF=
,
∴EF=
=
,
∴EF=EN,
∴以E点为圆心,EF为半径的⊙E与直线y=
相切.
②连接DF过点D作直线y=
的垂线,垂足为M.过点D作DQ⊥GH垂足Q,
则DM=QG=
-
=
=
.
在Rt△FQD中,QD=
,QF=
-
=
=2.FD=
=
.
∴以D点为圆心DF为半径的⊙D与直线y=
相切.
③以抛物线上任意一点P为圆心,以PF为半径的圆与直线y=
相切.
说明:解答题只提供了一种答案,如有其他解法只要正确,可参照本评分标准按步骤赋分.
 解:(1)设抛物线的解析式为y=ax2+bx+c,
解:(1)设抛物线的解析式为y=ax2+bx+c,且过点A(-3,0),C(0,3),E(1,0),
由(0,3)在y=ax2+bx+cH.
则c=3.
得方程组
|
解得a=-1,b=-2.
∴抛物线的解析式为y=-x2-2x+3.
(2)由y=-x2-2x+3=-(x+1)2+4,
得顶点坐标为(-1,4),对称轴为x=-1.
(3)①连接EF,过点E作直线y=
| 17 |
| 4 |
则EN=HG=
| 17 |
| 4 |
在Rt△FHE中,HE=2,HF=
| 15 |
| 4 |
∴EF=
| HE2+HF2 |
| 17 |
| 4 |
∴EF=EN,
∴以E点为圆心,EF为半径的⊙E与直线y=
| 17 |
| 4 |
②连接DF过点D作直线y=
| 17 |
| 4 |
则DM=QG=
| 17 |
| 4 |
| 7 |
| 4 |
| 10 |
| 4 |
| 5 |
| 2 |
在Rt△FQD中,QD=
| 3 |
| 2 |
| 15 |
| 4 |
| 7 |
| 4 |
| 8 |
| 4 |
| QF2+QD2 |
| 5 |
| 2 |
∴以D点为圆心DF为半径的⊙D与直线y=
| 17 |
| 4 |
③以抛物线上任意一点P为圆心,以PF为半径的圆与直线y=
| 17 |
| 4 |
说明:解答题只提供了一种答案,如有其他解法只要正确,可参照本评分标准按步骤赋分.
点评:本题考查了用待定系数法确定抛物线的解析式,及由抛物线的解析式求顶点坐标和对称轴的方法;
第3问利用构造直角三角形,勾股定理求线段的长,及定点到定直线的距离的求法;
最后的猜想实际是说明了抛物线是由到定点和定直线距离相等的点的集合.
第3问利用构造直角三角形,勾股定理求线段的长,及定点到定直线的距离的求法;
最后的猜想实际是说明了抛物线是由到定点和定直线距离相等的点的集合.

练习册系列答案
相关题目

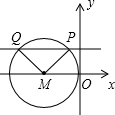 如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P,Q两点,点P在点Q的右方,若点P的坐标是(-1,2),有下列结论:①点Q的坐标是(-4,2);②PQ=3;③△MPQ的面积是3;④M点的坐标是(-3,0).其中正确的结论序号是
如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P,Q两点,点P在点Q的右方,若点P的坐标是(-1,2),有下列结论:①点Q的坐标是(-4,2);②PQ=3;③△MPQ的面积是3;④M点的坐标是(-3,0).其中正确的结论序号是 (2013•安庆二模)在平面直角坐标系中.过一点分別作x轴与y轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.给出以下结论:①点M(2,4)是和谐点;②不论a为何值时,点P(2,a)不是和谐点;③若点P(a,3)是和谐点,则a=6;④若点F是和谐点,则点F关于坐标轴的对称点也是和谐点.正确结论的序号是
(2013•安庆二模)在平面直角坐标系中.过一点分別作x轴与y轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.给出以下结论:①点M(2,4)是和谐点;②不论a为何值时,点P(2,a)不是和谐点;③若点P(a,3)是和谐点,则a=6;④若点F是和谐点,则点F关于坐标轴的对称点也是和谐点.正确结论的序号是 (2012•老河口市模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+c交y轴于A(0,4),交x轴于B、C两点(点B在点C的左侧).B、C两点坐标分别为(3,0),(8,0).
(2012•老河口市模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+c交y轴于A(0,4),交x轴于B、C两点(点B在点C的左侧).B、C两点坐标分别为(3,0),(8,0).