题目内容
【题目】如图,已知点A(0,2),B(2,2),C(﹣1,﹣2),抛物线F:y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P. 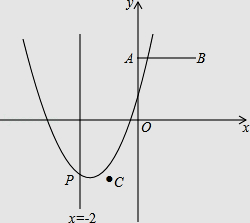
(1)当抛物线F经过点C时,求它的表达式;
(2)设点P的纵坐标为yP , 求yP的最小值,此时抛物线F上有两点(x1 , y1),(x2 , y2),且x1<x2≤﹣2,比较y1与y2的大小;
(3)当抛物线F与线段AB有公共点时,直接写出m的取值范围.
【答案】
(1)解:∵抛物线F经过点C(﹣1,﹣2),
∴﹣2=(﹣1)2﹣2×m×(﹣1)+m2﹣2,
解得,m=﹣1,
∴抛物线F的表达式是:y=x2+2x﹣1;
(2)解:当x=﹣2时,yp=4+4m+m2﹣2=(m+2)2﹣2,
∴当m=﹣2时,yp的最小值﹣2,
此时抛物线F的表达式是:y=x2+4x+2=(x+2)2﹣2,
∴当x≤﹣2时,y随x的增大而减小,
∵x1<x2≤﹣2,
∴y1>y2;
(3)解:m的取值范围是﹣2≤m≤0或2≤m≤4,
理由:∵抛物线F与线段AB有公共点,点A(0,2),B(2,2),
∴ ![]() 或
或 ![]() 或
或 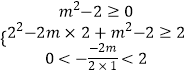 ,
,
解得,﹣2≤m≤0或2≤m≤4.
【解析】(1)根据抛物线F:y=x2﹣2mx+m2﹣2过点C(﹣1,﹣2),可以求得抛物线F的表达式;(2)根据题意,可以求得yP的最小值和此时抛物线的表达式,从而可以比较y1与y2的大小;(3)根据题意可以列出相应的不等式组,从而可以解答本题

练习册系列答案
相关题目