题目内容
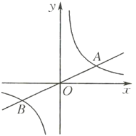
【题目】如图，在平面直角坐标系中，将
绕点A顺时针旋转到
的位置，点B、O分别落在点
、
处，点在x轴上，再将绕点顺时针旋转到
的位置，点
在x轴上，将绕点顺时针旋转到
的位置，点
在x轴上，依次进行下去
若点
，
，则点
的坐标为______．
【答案】
【解析】
根据勾股定理求得AB，再根据旋转的性质求OC2的值以及B2，B4的坐标，找到规律，即可求出答案．
解：∵OA=
，OB=2，
∴AB=
=
=
，
根据旋转的性质得：OA=A2C2=A4C4=，
OB= B1C2=B2C2=B4C4=2，
AB=AB1=A2B3=，
∴OA+AB1+B1C2=++2=6，
∴点B2的横坐标为6，纵坐标为2，即B2（6，2），
由图可知，OC4=2（OA+AB1+B1C2）=2×6=12，
∴点B4的横坐标为12，纵坐标为2，即B4（12，2），
以此类推可得，B2016的横坐标为：
OC2016=
（OA+AB1+B1C2）=1008×6=6048，
∴点B2016的横坐标为6048，纵坐标为2，即B2016（6048，2）。
故答案为：（6048,2）．
练习册系列答案
相关题目
【题目】为了发展学生的核心素养，培养学生的综合能力，某中学利用“阳光大课间”，组织学生积极参加丰富多彩的课外活动，学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等，其中射击队在某次训练中，甲、乙两名队员各射击10发子弹，成绩记录如表：
射击次序（次） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲的成绩（环） | 8 | 9 | 7 | 9 | 8 | 6 | 7 | a | 10 | 8 |
乙的成绩（环） | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
（1）经计算甲和乙的平均成绩是8（环），请求出表中的a＝ ；
（2）甲成绩的中位数是 环，乙成绩的众数是 环；
（3）若甲成绩的方差是1.2，请求出乙成绩的方差，判断甲、乙两人谁的成绩更为稳定？
