题目内容
【题目】商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为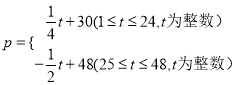 ,且其日销售量y(kg)与时间t(天)的关系如下表:
,且其日销售量y(kg)与时间t(天)的关系如下表:

(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
【答案】(1)y=-2t+120,当t=30时,y=60(kg)
(2)当t=10时,W最大=1250元
【解析】试题分析:(1)设y=kt+b,利用待定系数法即可解决问题.(2)日利润=日销售量×每公斤利润,据此分别表示前24天和后24天的日利润,根据函数性质求最大值后比较得结论.
试题解析:(1)设y=kt+b,把t=1,y=118;t=3,y=114代入得到:
![]() ,解得
,解得![]() ,
,
∴y=2t+120.
将t=30代入上式,得:y=2×30+120=60.
所以在第30天的日销售量是60kg.
(2)设第x天的销售利润为w元。
当1t24时,由题意w=(2t+120)( ![]() t+3020)=
t+3020)= ![]() (t10)2+1250,
(t10)2+1250,
∴t=10时w最大值为1250元。
当25t48时,w=(2t+120)(( ![]() t+4820)=t2116t+3360,
t+4820)=t2116t+3360,
∵对称轴t=58,a=1>0,
∴在对称轴左侧w随x增大而减小,
∴t=25时,w最大值=1085,
综上所述第10天利润最大,最大利润为1250元。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目