题目内容
【题目】如图,在△ABC中,AB=AC=5,P是BC边上除点B、C外的任意一点,则AP2+PBPC= . 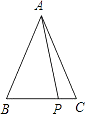
【答案】25
【解析】解:过点A作AD⊥BC于D,
∵AB=AC=5,∠ADP=∠ADB=90°,
∴BD=CD,PA2=PD2+AD2 , AD2+BD2=AB2 ,
∴AP2+PBPC=AP2+(BD+PD)(CD﹣PD)=AP2+(BD+PD)(BD﹣PD)=AP2+BD2﹣PD2=AP2﹣PD2+BD2=AD2+BD2=AB2=25.
故答案为25.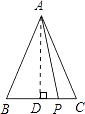
首先过点A作AD⊥BC于D,可得∠ADP=∠ADB=90°,又由AB=AC,根据三线合一的性质,可得BD=CD,由勾股定理可得PA2=PD2+AD2 , AD2+BD2=AB2 , 然后由AP2+PBPC=AP2+(BD+PD)(CD﹣PD),即可求得答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目