Question

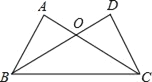
【题目】如图，在△ABC和△DCB中，∠BAC=∠CDB=90°，AB=DC，AC与BD交于点O．

（1）求证：△ABC≌△DCB．

（2）当∠DBC=30°，BC=6时，求BO的长．

Answer 1

【答案】（1）证明见解析；（2）BO=2．

【解析】

（1）通过“HL”即可证明Rt△ABC≌Rt△DCB；

（2）在△BCD中利用三角形函数可得CD=3，BD=3，在△OCD中，利用三角形函数可得OD=CD=，则OB=BD﹣OD=2．

（1）在△ABC和△DCB中，∠A=∠D=90°，

，

∴△ABC≌△DCB（HL）；

（2）∵∠BDC=90°，∠DBC=30°，BC=6，

∴CD=3，BD=3，

∵∠DOC=∠DBC+∠ACB=60°，

∴OD=CD=，

∴OB=BD﹣OD=2．