题目内容
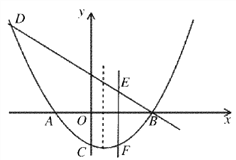
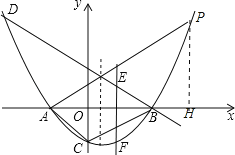
【题目】如图,已知拋物线![]() (k为常数,且k>0)与x轴的交点为A、B,与y轴的交点为C,经过点B的直线
(k为常数,且k>0)与x轴的交点为A、B,与y轴的交点为C,经过点B的直线![]() 与抛物线的另一个交点为D.
与抛物线的另一个交点为D.
(1)若点D的横坐标为x= -4,求这个一次函数与抛物线的解析式;
(2)若直线m平行于该抛物线的对称轴,并且可以在线段AB间左右移动,它与直线BD和抛物线分别交于点E、F,求当m移动到什么位置时,EF的值最大,最大值是多少?
(3)问原抛物线在第一象限是否存在点P,使得△APB∽△ABC?若存在,请求出这时k的值;若不存在,请说明理由.
【答案】(1) ![]() (2) 最大值是4(3)存在
(2) 最大值是4(3)存在
【解析】分析:(1)先解方程k(x+2)(x﹣4)=0可得A(﹣2,0),B(4,0),再把B点坐标代入y=﹣![]() x+b中求出得b=2,则可得到一次函数解析式为y=﹣
x+b中求出得b=2,则可得到一次函数解析式为y=﹣![]() x+2,接着利用一次函数解析式确定D点坐标,然后把D点坐标代入代入y=k(x+2)(x﹣4)中求出k的值即可得到得抛物线解析式;
x+2,接着利用一次函数解析式确定D点坐标,然后把D点坐标代入代入y=k(x+2)(x﹣4)中求出k的值即可得到得抛物线解析式;
(2)利用二次函数和一次函数图象上点的坐标特征,可设F(t,![]() t2﹣
t2﹣![]() t﹣2),则E(t,﹣
t﹣2),则E(t,﹣![]() t+2),﹣2≤t≤4,于是得到EF=﹣
t+2),﹣2≤t≤4,于是得到EF=﹣![]() t+2﹣(
t+2﹣(![]() t2﹣
t2﹣![]() t﹣2)=﹣
t﹣2)=﹣![]() t2+4,然后根据二次函数的性质求解;
t2+4,然后根据二次函数的性质求解;
(3)作PH⊥x轴于H,如图,先表示出C点坐标为(0,﹣8k),设P[n,k(n+2)(n﹣4)],根据相似三角形的判定方法,当∠PAB=∠CAB,AP:AB=AB:AC时,△APB∽△ABC;再根据正切定义.在Rt△APH中有tan∠PAH=![]() .在Rt△OAC中有tan∠OAC=
.在Rt△OAC中有tan∠OAC=![]() =4k,则
=4k,则![]() =4k,解得n=8,于是得到P(8,40k),接着利用勾股定理计算出AP=10
=4k,解得n=8,于是得到P(8,40k),接着利用勾股定理计算出AP=10![]() ,AC=2
,AC=2![]() ,然后利用AP:AB=AB:AC得到10
,然后利用AP:AB=AB:AC得到10![]() 2
2=62,解得k1=
![]() ,k2=﹣
,k2=﹣![]() (舍去),于是可确定P点坐标.
(舍去),于是可确定P点坐标.
详解:(1)当y=0时,k(x+2)(x﹣4)=0,解得:x1=﹣2,x2=4,则A(﹣2,0),B(4,0),把B(4,0)代入y=﹣![]() x+b得:﹣2+b=0,解得:b=2,所以一次函数解析式为y=﹣
x+b得:﹣2+b=0,解得:b=2,所以一次函数解析式为y=﹣![]() x+2,当x=﹣4时,y=﹣
x+2,当x=﹣4时,y=﹣![]() x+2=4,则D点坐标为(4,4),把D(﹣4,4)代入y=k(x+2)(x﹣4)得:k(﹣2)(﹣8)=4,解得:k=
x+2=4,则D点坐标为(4,4),把D(﹣4,4)代入y=k(x+2)(x﹣4)得:k(﹣2)(﹣8)=4,解得:k=![]() ,所以抛物线解析式为y=
,所以抛物线解析式为y=![]() (x+2)(x﹣4),即y=
(x+2)(x﹣4),即y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
(2)设F(t,![]() t2﹣
t2﹣![]() t﹣2),则E(t,﹣
t﹣2),则E(t,﹣![]() t+2),﹣2≤t≤4,所以EF=﹣
t+2),﹣2≤t≤4,所以EF=﹣![]() t+2﹣(
t+2﹣(![]() t2﹣
t2﹣![]() t﹣2)=﹣
t﹣2)=﹣![]() t2+4,所以当t=0时,EF最大,最大值为4,即当直线m移动到与y轴重合的位置时,EF的值最大,最大值是4;
t2+4,所以当t=0时,EF最大,最大值为4,即当直线m移动到与y轴重合的位置时,EF的值最大,最大值是4;
(3)存在.
作PH⊥x轴于H,如图,当x=0时,y=k(x+2)(x﹣4)=﹣8k,则C(0,﹣8k),设P[n,k(n+2)(n﹣4)],当∠PAB=∠CAB,AP:AB=AB:AC时,△APB∽△ABC;
在Rt△APH中,tan∠PAH=![]() .在Rt△OAC中,tan∠OAC=
.在Rt△OAC中,tan∠OAC=![]() =4k,∴
=4k,∴![]() =4k,解得:n=8,则P(8,40k),∴AP=
=4k,解得:n=8,则P(8,40k),∴AP=![]() =
=![]() =10
=10![]() ,而AC=
,而AC=![]() =
=![]() =2
=2![]() .∵AP:AB=AB:AC,∴APAC=AB2,即10
.∵AP:AB=AB:AC,∴APAC=AB2,即10![]() 2
2![]() =62,∴5(16k2+1)=9,解得:k1=
=62,∴5(16k2+1)=9,解得:k1=![]() ,k2=﹣
,k2=﹣![]() (舍去),∴k=4
(舍去),∴k=4![]() ,P点坐标为(8,4
,P点坐标为(8,4![]() ).
).

 金钥匙试卷系列答案
金钥匙试卷系列答案