Question

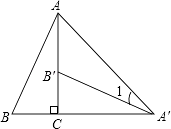
【题目】如图，某山顶上建有手机信号中转塔AB，在地面D处测得塔尖的仰角∠ADC=60°，塔底的仰角∠BDC=45°，点D距离塔AB所在直线的距离DC为100米，求手机信号中转塔AB的高度（参考数据： ≈1.414， ≈1.732，结果保留整数）．

Answer 1

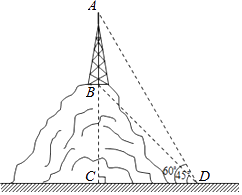
【答案】解：由题意可知，△ACD与△BCD都是直角三角形．
在Rt△BCD中，∵∠BDC=45°，
∴BC=CD=100米．
在Rt△ACD中，∵∠ADC=60°，CD=100米，
∴tan∠ADC= ，即 = ，
∴AC=100 ，
∴AB=AC﹣BC=100（ ﹣1）≈73（米）．
答：手机信号中转塔的高度约为73米
【解析】先在Rt△BCD中，根据∠BDC=45°，得出BC=CD=100；再在Rt△ACD中，根据正切函数的定义，求出AC=100 ，然后由AB=AC﹣BC即可求解．
【考点精析】本题主要考查了关于仰角俯角问题的相关知识点，需要掌握仰角：视线在水平线上方的角；俯角：视线在水平线下方的角才能正确解答此题．