题目内容
【题目】如图,在△ABC中,以AB为直径的⊙O分别交AC,BC于点D,E.连接ED,若ED=EC.
(1)求证:AB=AC;
(2)填空:①若AB=6,CD=4,则BC=;
②连接OD,当∠A的度数为时,四边形ODEB是菱形.
【答案】
(1)
证明:∵ED=EC,
∴∠EDC=∠C,
∵∠EDC=∠B,
∴∠B=∠C,
∴AB=AC;
(2)2 ![]() ;60°
;60°
【解析】(2)解:①连接AE,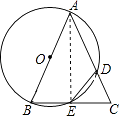
∵AB为直径,
∴AE⊥BC,
由(1)知AB=AC=6,
∵∠C=∠C,∠CDE=∠B,
∴△CDE∽△CBA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BC=2 ![]() ,
,
所以答案是:2 ![]() ;(3)当∠A=60°时,四边形ODEB是菱形,
;(3)当∠A=60°时,四边形ODEB是菱形,
∵∠A=60°,
∴∠BAE=30°,
∵∠AEB=90°,
∴BE= ![]() AD=BO,
AD=BO,
∴BE=DE=OB=OD,
∴四边形ODEB是菱形,
所以答案是:60°.
【考点精析】根据题目的已知条件,利用菱形的判定方法和圆周角定理的相关知识可以得到问题的答案,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目








