题目内容
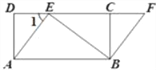
【题目】如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF．
（1）求证：四边形ABFE是平行四边形；
（2）若∠BEF=∠DAE,AE=3,BE=4,求EF的长．
【答案】（1）证明见解析（2）EF=AB=5．
【解析】（1）证明：∵四边形ABCD是矩形，∴AD=BC，∠D=∠BCD=90°．
∴∠BCF=180°﹣∠BCD=180°﹣90°=90°．
∴∠D=∠BCF．在Rt△ADE和Rt△BCF中，
∴Rt△ADE≌Rt△BCF．
∴∠1=∠F．∴AE∥BF．∵AE=BF，∴四边形ABFE是平行四边形．
（2）解：∵∠D=90°，∴∠DAE+∠1=90°．∵∠BEF=∠DAE，∴∠BEF+∠1=90°．
∵∠BEF+∠1+∠AEB=180°，∴∠AEB=90°．
在Rt△ABE中，AE=3，BE=4，AB=
．
∵四边形ABFE是平行四边形，∴EF=AB=5．
练习册系列答案
相关题目
