题目内容
【题目】如图，在△ABC中，∠ACB=90°，AC=BC，延长AB至点D，使DB=AB，连接CD，以CD为直角边作等腰直角三角形CDE，其中∠DCE=90°，连接BE.
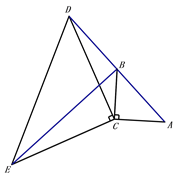
（1）求证：△ACD≌△BCE；
（2) 若AC=3cm，求BE的长度.
【答案】（1）详见解析；（2）
.
【解析】试题分析：（1）根据等腰直角三角形的性质得到
然后利用“SAS”可判断
≌
即可；
（2）根据全等三角形的性质得到
即可；
试题解析：(1)证明：∵△CDE是等腰直角三角形, 
∴CD=CE，
∴∠ACB=∠DCE，
∴∠ACB+∠BCD=∠DCE+∠BCD，
∴∠ACD=∠BCE，
在△ACD和△BCE中,
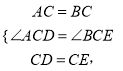
∴△ACD≌△BCE(SAS)；
(2) 
由勾股定理得: 
又
∵
≌
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】尺规作三角形的类型：
尺 规 作 图 | 类型 | 依据 |
已知两边及其夹角作三角形 | __________ | |
已知两角一边作三角形 | __________（或 | |
已知三边作三角形 | __________ |
【答案】 SAS ASA SSS
【解析】试题解析：已知两边及其夹角作三角形,其依据是：SAS.
已知两角一边作三角形,其依据是：ASA（或
）.
已知三边作三角形, 其依据是： 
故答案为： 
点睛：判定三角形全等的方法有： 
【题型】填空题
【结束】
11
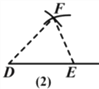
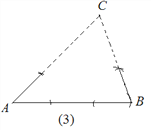
【题目】如图，根据图中作图痕迹，可以得出作三角形的依据分别是：
（1）__________；
（2）___________；
（3）__________.（图中虚线表示最后作出的线段）
