题目内容
【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象的顶点为D,与y轴交于点C,与x轴交于A、B两点,点A在原点的左侧,点B的坐标为(3,0),OB=OC=3OA.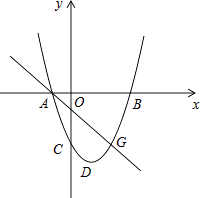
(1)求这个二次函数的解析式;
(2)如图,若点G(2,m)是该抛物线上一点,E是直线AG下方抛物线上的一动点,当点E运动到什么位置时,△AEG的面积最大?求此时点E的坐标和△AEG的最大面积;
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆的半径.
【答案】
(1)
解:由已知得:C(0,﹣3),A(﹣1,0)
将A、B、C三点的坐标代入得 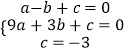
解得: 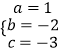
所以这个二次函数的表达式为:y=x2﹣2x﹣3
(2)
解:当x=2时,y=x2﹣2x﹣3=﹣3,即G(2,﹣3),
设AG的解析式为y=kx+b,将A、G代入函数解析式,得
![]() ,解得
,解得 ![]() ,
,
直线AG的解析式为y=﹣x﹣1.
过E作EF⊥x轴交AG于,F如图1
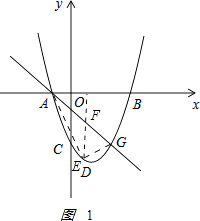 ,
,
E在抛物线上,F在直线AG上,
设E点坐标为(n,n2﹣2n﹣3),F(n,﹣n﹣1),
EF=(﹣n﹣1)﹣(n2﹣2n﹣3)=﹣n2+n+2
S= ![]() EF(G﹣xA)=
EF(G﹣xA)= ![]() ×(﹣n2+n+2)[2﹣(﹣1)]
×(﹣n2+n+2)[2﹣(﹣1)]
=﹣ ![]() (n﹣
(n﹣ ![]() )2+
)2+ ![]() ,
,
当n= ![]() 时,S最大值是
时,S最大值是 ![]() ,
,
n2﹣2n﹣3=﹣ ![]() ,即E(
,即E( ![]() ,﹣
,﹣ ![]() )
)
(3)
解:如图2
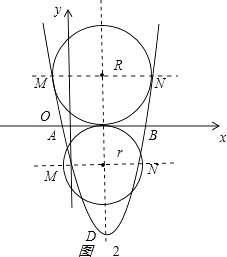 ,
,
① 当直线MN在x轴上方时,设圆的半径为R(R>0),则N(R+1,R),
代入抛物线的表达式,解得R= ![]() ;
;
②当直线MN在x轴下方时,设圆的半径为r(r>0),则N(r+1,﹣r),
代入抛物线的表达式,解得r= ![]() ,
,
∴圆的半径为 ![]() 或
或 ![]()
【解析】(1)根据已知条件,易求得C、A的坐标,可用待定系数法求出抛物线的解析式;(2)可分别过E、G作x轴的垂线,设垂足为F、H;那么△AGE的面积=△AEF的面积+四边形FHGE的面积﹣△AGH的面积,设出E点的坐标,即可表示出F点坐标及EF的长,根据上面所得出的面积计算方法,可得出关于△AGE的面积与E点横坐标的函数关系式,根据所得函数的性质,即可求出△AGE的最大面积及对应的E点坐标;(3)根据抛物线和圆的对称性,知圆心必在抛物线的对称轴上,由于该圆与x轴相切,可用圆的半径表示出M、N的坐标,将其入抛物线的解析式中,即可求出圆的半径;(需注意的是圆心可能在x轴上方,也可能在x轴下方,需要分类讨论)
【考点精析】掌握二次函数的图象和二次函数的性质是解答本题的根本,需要知道二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 名校课堂系列答案
名校课堂系列答案【题目】某车 间生产一批圆柱形机器零件,从中抽出了 6 件进行检验,把标准直径的长记为 0,比标准直径长的记为正数,比标准直径短的记为负数,检查记录如下:
1 | 2 | 3 | 4 | 5 | 6 |
+0.2 | ﹣0.3 | ﹣0.2 | +0.3 | +0.4 | ﹣0.1 |
则第_________个零件最符合标准.