题目内容
【题目】一个几何体是由若干个棱长为3cm的小正方体搭成的,从左面、上面看到的几何体的形状图如图所示:
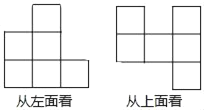
(1)该几何体最少由 个小立方体组成,最多由 个小立方体组成.
(2)将该几何体的形状固定好,
①求该几何体体积的最大值;
②若要给体积最小时的几何体表面涂上油漆,求所涂油漆面积的最小值.
【答案】(1)9,14;(2)①答案见解析,②答案见解析.
【解析】
(1)由俯视图可得该几何体的最底层的立方体的个数;由左视图第一列至第三列的正方形的个数可得该几何体最少和最多的立方体的个数;(2)①由(1)求最多立方体个数时该几何体的最大值;②由(1)求最少立方体个数时几何体的表面积.
解:(1)观察图象可知:最少的情形有2+3+1+1+1+1=9个小正方体,
最多的情形有2+2+3+3+3+1=14个小正方体.
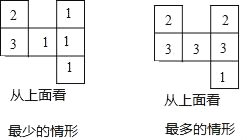
故答案为9,14.
(2)①该几何体体积的最大值为33×14=378cm3.
②体积最小时的几何体表面涂上油漆,共需涂36个面,所涂油漆面积的最小值=9×36=324cm2.

练习册系列答案
相关题目