Question

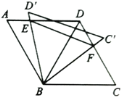
【题目】如图，四边形是面积为的平行四边形，其中.

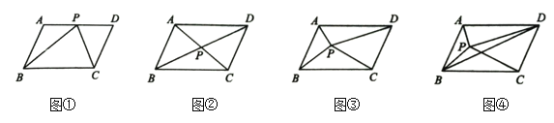
（1）如图①，点为边上任意一点，则的面积和的面积之和与的面积之间的数量关系是__________；

（2）如图②，设交于点，则的面积和的面积之和与的面积之间的数量关系是___________；

（3）如图③，点为内任意一点时，试猜想的面积和的面积之和与的面积之间的数量关系，并加以证明；

（4）如图④，已知点为内任意一点，的面积为，的面积为，连接，求的面积.

Answer 1

【答案】（1）； （2）； （3）结论：；理由见解析；（4）6

【解析】

（1）根据平行四边形的性质可知：，即可解决问题；

（2）理由平行四边形的性质可知：，即可解决问题；

（3）结论：．如图③中，作于，延长交于．根据；

（4）设的面积为，的面积为，则，推出，可得的面积；

解：（1）如图①中，，．

四边形是平行四边形，

，

，

，

．

故答案为．

（2）如图②中，四边形是平行四边形，

，，

，

．

故答案为．

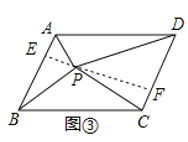
（3）结论：．

理由：如图③中，作于，延长交于．

，，

，

．

（4）设的面积为，的面积为，

则，

，

的面积，