题目内容
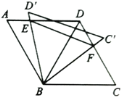
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G.F为AB边上一点,连接CF,且∠ACF=∠CBG.
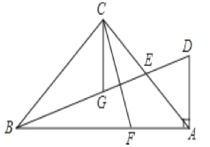
(1)求证:BG=CF;
(2)求证:CF=2DE;
(3)若DE=1,求AD的长
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)利用“ASA”判断△BCG≌△CFA,从而得到BG=CF;
(2)连结AG,利用等腰直角三角形的性质得CG垂直平分AB,则BG=AG,再证明∠D=∠GAD得到AG=DG,所以BG=DG,接着证明△ADE≌△CGE得到DE=GE,则BG=2DE,利用利用△BCG≌△CFA得到CF=BG,于是有CF=2DE;
(3)先得到BG=2,GE=1,则BE=3,设CE=x,则BC=AC=2CE=2x,在Rt△BCE中利用勾股定理得到x![]() +(2x)
+(2x)![]() =3
=3![]() ,解得x=
,解得x=![]() ,所以BC=
,所以BC=![]() ,AB=
,AB=![]() BC=
BC=![]() ,然后在Rt△ABD中利用勾股定理计算AD的长.
,然后在Rt△ABD中利用勾股定理计算AD的长.
(1)证明:∵∠ACB=90°,AC=BC,
∴△ACB为等腰直角三角形,
∴∠CAF=∠ACG=45°,
∵CG平分∠ACB,
∴∠BCG=45°,
在△BCG和△CFA中
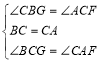 ,
,
∴△BCG≌△CFA,
∴BG=CF;
(2)证明:连结AG,
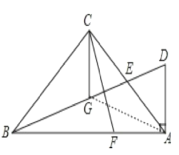
∵CG为等腰直角三角形ACB的顶角的平分线,
∴CG垂直平分AB,
∴BG=AG,
∴∠GBA=∠GAB,
∵AD⊥AB,
∴∠D+∠DBA=90°,∠GAD+∠GAB=90°,
∴∠D=∠GAD,
∴AG=DG,
∴BG=DG,
∵CG⊥AB,DA⊥AB,
∴CG∥AD,
∴∠DAE=∠GCE,
∵E为AC边的中点,
∴AE=CE,
在△ADE和△CGE中
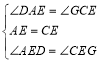 ,
,
∴△ADE≌△CGE,
∴DE=GE,
∴DG=2DE,
∴BG=2DE,
∵△BCG≌△CFA,
∴CF=BG,
∴CF=2DE;
(3)∵DE=1,
∴BG=2,GE=1,即BE=3,
设CE=x,则BC=AC=2CE=2x,
在Rt△BCE中,x![]() +(2x)
+(2x) ![]() =3
=3![]() ,解得x=
,解得x=![]() ,
,
∴BC=![]() ,
,
∴AB=![]() BC=
BC=![]() ,
,
在Rt△ABD中,∵BD=4,AB=![]() ,
,
∴AD=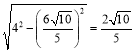 .
.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】小颖和小红两位同学在做投掷骰子(质地均匀的正方体)实验,他们共做了![]() 次实验,实验的结果如下:
次实验,实验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
(1)计算“![]() 点朝上”的频率和“
点朝上”的频率和“![]() 点朝上”的频率.
点朝上”的频率.
(2)小颖说:“根据实验得出,出现![]() 点朝上的机会最大”;小红说:“如投掷
点朝上的机会最大”;小红说:“如投掷![]() 次,那么出现
次,那么出现![]() 点朝上的次数正好是
点朝上的次数正好是![]() 次.”小颖和小红的说法正确吗?为什么?
次.”小颖和小红的说法正确吗?为什么?