��Ŀ����
����Ŀ���Ķ����⣺����һ�����Σ����������һ�����Σ������ܳ�������ֱ�����֪���ε��ܳ��������2��������������Ǹ������ε����ӱ�������.��ͼ������![]() �Ǿ���
�Ǿ���![]() �����ӱ�������.
�����ӱ�������.

������⣺
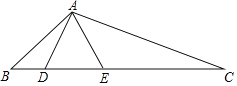
��1�������εij��Ϳ��ֱ�Ϊ3��2ʱ�����Ƿ�������ӱ������Σ������ڣ�������ӱ������εij�������������ڣ���˵������.
��2���߳�Ϊ![]() �������δ������ӱ������������������жϣ���˵������.
�������δ������ӱ������������������жϣ���˵������.
���𰸡���1�����ڣ�����������2�������ڣ�������.
��������
(1) �����ӱ������ε�һ��Ϊ![]() ������һ��Ϊ
������һ��Ϊ![]() ,�����������֪���������2���г�����,��⼴�ɣ���2���������⣺������������������ͼ�Σ���������ͼ�ε����ʣ�����������Ʊȼ��ܳ��ȵ�ƽ�����ʲ��������ӱ��������Σ�
,�����������֪���������2���г�����,��⼴�ɣ���2���������⣺������������������ͼ�Σ���������ͼ�ε����ʣ�����������Ʊȼ��ܳ��ȵ�ƽ�����ʲ��������ӱ��������Σ�
��1���⣺����
�����ӱ������ε�һ��Ϊ![]() ������һ��Ϊ
������һ��Ϊ![]() ��
��
��![]() ��
��
��֮�ã�![]() ��
��![]() ��
��
��![]() ����
����![]() ��
��
�����ӱ������εij�Ϊ![]() ����Ϊ
����Ϊ![]() ��
��
��2�������ڣ�
��Ϊ����������������ͼ�Σ������ǵ��ܳ���Ϊ2ʱ��
������ȱض���4�����Բ�����.

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ