题目内容
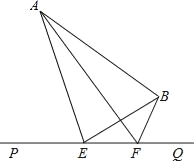
【题目】如图,点D,E在线段BC上,△ADE是等边三角形,且∠BAC=120°
(1)求证:△ABD∽△CAE;
(2)若BD=2,CE=8,求BC的长.

【答案】(1)证明见解析;(2)14.
【解析】
(1)根据等边三角形的性质、三角形的外角的性质得到∠B=∠EAC,∠ADB=∠AEC,根据相似三角形的判定定理证明结论;
(2)根据相似三角形的性质列出比例式,计算即可.
(1)证明:∵∠BAC=120°,
∴∠BAD+∠EAC=60°,
∵△ADE是等边三角形,
∴∠ADE=∠AED=60°,
∴∠BAD+∠B=60°,∠ADB=∠AEC=120°,
∴∠B=∠EAC,又∠ADB=∠AEC,
∴ABD∽△CAE;
(2)解:∵△ABD∽△CAE,
∴![]() =
=![]() ,即AD2=BDCE=16,
,即AD2=BDCE=16,
解得,AD=4,则DE=4,
∴BC=BD+DE+EC=14.

练习册系列答案
相关题目