题目内容
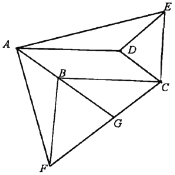
【题目】如图,在口ABCD中,分别以边BC,CD作等腰△BCF,△CDE,使BC=BF,CD=DE,∠CBF=∠CDE,连接AF,AE.
(1)求证:△ABF≌△EDA;
(2)延长AB与CF相交于G,若AF⊥AE,求证BF⊥BC.
【答案】(1)证明见解析;(2)证明见解析.
【解析】(1)证明AB=DE,FB=AD,∠ABF=∠ADE即可解决问题;
(2)只要证明FB⊥AD即可解决问题.
详(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠ABC=∠ADC,
∵BC=BF,CD=DE,
∴BF=AD,AB=DE,
∵∠ADE+∠ADC+∠EDC=360°,∠ABF+∠ABC+∠CBF=360°,∠EDC=∠CBF,
∴∠ADE=∠ABF,
在△ABF与△EDA中,
∵AB=DE,∠ABF=∠ADE,BF=AD
∴△ABF≌△EDA.
(2)证明:延长FB交AD于H.
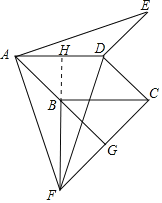
∵AE⊥AF,
∴∠EAF=90°,
∵△ABF≌△EDA,
∴∠EAD=∠AFB,
∵∠EAD+∠FAH=90°,
∴∠FAH+∠AFB=90°,
∴∠AHF=90°,即FB⊥AD,
∵AD∥BC,
∴FB⊥BC.

练习册系列答案
相关题目